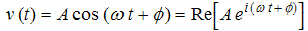Complex Phasors

---

A complex representation of oscillations - complex phasors

We'll start off by repeating Euler's formula and our cosine formula for a wave:

.

We see that the real part of e^ix has a cosine in it just like the oscillating cosine equation above. To connect the two concepts, we use the fact that the real part of the right side of Euler's formula is the cos x. Thus, we can write the second equation as:

,

where the "Re" in the equation stands for "real part of". Some authors use the symbol ℜ for this instead of Re. The real part of a complex number is the term or terms that do not contain an i. Often the phase shift ϕ is incorporated into the constant A as:

,

where

. We can view this new A, with a tilde on it, as a complex amplitude, containing both the strength or amplitude of the oscillations, and also the phase shift ϕ.

An animated phasor diagram showing temporal behavior of e^iωt. The box in the top left corner shows the frequency, angular frequency, time, and angular position of the vector (both in radians and degrees). Notice how t and ωt both increase as the animation runs. Also notice that ωt corresponds to the polar angle of the vector at any time, i.e. that when ωt = 180 degrees or about 3 radians, the pink vector is pointed left at the 3 radian mark. The projection (or shadow) on the floor represents the real part of e^iωt.

The frequency, f, is the number of complete rotations the vector makes per second. The angular frequency, ω, is just f times 2π. The frequency of oscillation does not necessarily correspond exactly to the frequency of oscillation of the shadow you observe on your computer because of variations from computer to computer.

Mouse over the animation to start it and mouse off to stop it. Click on the animation to restart the time, t, from zero. Every time it is restarted, a different frequency is used. Notice that when the frequency is lower, the rotational speed is lower.

This animation is very similar to one used earlier for phasors. After all, the concept of phasors is very, very similar to these plots on the complex plane of terms with e^iωt in them. The advantage of the complex notation over phasors is that complex notation gives us a powerful algebraic notation for oscillations and waves.

Press − in the +/− button to hid the cartoon features of this animation and + to restore them. This animation can be downloaded free at George Mason University Archival Repository. Please read the fair use policy for this work.

e^iωt is a real show shopper ... the central genius of the complex representation of oscillations.

What about the e^iωt term? A couple of pages ago, we discussed e^{i ϕ} and found that it represented a vector in the complex plane that started at the origin and had a length of one (or 1). It made a polar angle of ϕ with the real (or x) axis.

Now we are replacing the ϕ with ωt. The time factor, t, constantly increases making the product iωt also to constantly increase with time. The iωt is the polar angle in e^iωt, meaning that the polar angle increases with time. Thus the complex point representing e^iωt on the complex plane will be moving around in a circle of radius 1. As above, we usually add a vector from the origin to the point, just to help with the visualization.

We show this in the animation to the right. When ωt is larger than 360 degrees (6.28 radians) then the vector starts a new trip around the circle. After all an angle of 360 degrees is equivalent to 0 degrees in most situations.

Below we show another animation of an oscillating parameter expressed as the complex equation

.

The animation shows the relationship between the rotating complex vector, the oscillating voltage, and the graph of the voltage versus time. Notice here that the horizontal axis indicates time. We might have also labeled the horizontal axis as ωt with numbers ranging from 0 degrees to about 1600 degrees (or the corresponding radians) which is about 4.3 complex cycles.

An animated diagram showing the relationship between the rotating vector on the complex plane, the value of the oscillating parameter, and a graph of this parameter versus time. The complex plane has been rotated by 90 degrees to facilitate plotting the real component of the complex vector. The center object is a bar graph of the parameter modeled. In this case, we labeled the graph with "voltage" to indicate we are modeling an oscillating voltage, perhaps the voltage in a person's house, or in some electronic device (very much slowed down from most real electric oscillations). Notice that the voltage oscillates with time.

Mouse over the animation to activate it and mouse off to suspend its operation. Click it to reset the animation to zero.

This animation is set up with the rotor angle marked in degrees. Engineers often use degrees as an alternative to radians for simpler problems, remembering to switch back to radians for more difficult calculations. The usual notation is as:

.

For example, an oscillating voltage with an amplitude of 30 volts and an phase angle of 60 degrees might be written as:

.

This animation is extremely similar to an earlier one using phasors. You might be wondering, what is new? Why repeat all this stuff? I'm here to tell you that there is a very important new addition. In fact there are two new things here:

• We are using complex numbers and the complex plane now, and
• We have nice complex notation for the oscillation to allow us to solve equations involving oscillations and their parameters.

Press − in the +/− button to hid the cartoon features of this animation and + to restore them. This animation can be downloaded free at George Mason University Archival Repository. Please read the fair use policy for this work.

With deference to Leonardo da Vinci, pioneering artist, scientist, and inventor.

---

Multiplication of an oscillation by a complex constant

There are many physical phenomena and electrical circuit elements that change the amplitude and phase of an oscillation or wave by a fixed amount. Without using complex notation, there is no convenient way to mathematically express this. However with the use of the complex notation, this operation is merely multiplication by a complex constant. To further understand this, consider the following multiplication of an oscillation by the complex constant B:

    .

Here we see that the resulting product has an amplitude equal to the product of amplitudes, and the phase of the constant adds to the phase of the oscillation by the constant amount ϕ. We can compare this with a similar observation above which concerned multiplication of two complex constants. Here one of the factors has the e^iωt term which makes the resulting phase of the oscillation continue to increase with time. After the multiplication, the phase of the rotating vector is shifted by the fixed angle ϕ. In the animation below, we see this shift and the effect of the oscillations, which of course are just the real part of the rotating complex vectors.

An animated diagram showing the multiplication of a complex oscillation by the complex constant B. The value (amplitude and phase) of B, the multiplying complex constant is given in black at the top left of the animation. Note that B is written in the format discussed at the end of the caption in the animation just above. The yellow vector represent the initial oscillation, and the orange vector represents the product of the yellow vector (or oscillation) multiplied by B.

Mouse over the animation to activate it. Clicking it will reset the animation to zero. Each time the animation is reset, a new value for B is generated.

Stop the motion (by mousing off it) and study the phase relationship of the parts. The orange product or output vector leads the yellow input vector by the angle shown at the top of the animation. The output vector has had its phase increased by the phase of B. Thus if B has a positive phase then on the graph, the orange curve will reach the crests before the yellow curve of the input vector.

The vertical axis on the graph is labeled "temperature" and represents oscillation in the temperatures of two sensors. Perhaps the yellow sensor is in the water and the orange sensor is in the air above the water which is heated by the water. The period of oscillation would be one day, meaning that the animation is very much speeded up. While the animation is obviously a simplification, it is meant to illustrate a type of linked oscillations that can be mathematically modeled by the complex notation discussed here. In the center of the animation are bar graphs of the oscillating temperatures.

To sum up, this animation illustrates the time behavior of an oscillation modeled in the complex plane AND a second oscillation which results from multiplying the first oscillation by a complex constant. In general this results in an amplitude change and phase change.

Press − in the +/− button to hid the cartoon features of this animation and + to restore them. This animation can be downloaded free at George Mason University Archival Repository. Please read the fair use policy for this work.

In praise of summer beaches

A sampling of applications of multiplying an oscillation or wave by a complex constant

In each, the final signal, oscillation, or wave can be calculated by multiplying the initial signal by the appropriate complex constant.

• Microphone signal passing through a stereo amplifier.
• Telephone signal passing through 3 miles of wire.
• Fiber optic signal passing through in-line amplifier.
• Sound passing through the bone structure of the inner ear.
• AC power passing through transformers in residential transformers.
• Sound impinging on a microphone and converted to an electrical signal.
• Radar wave impinging on an airplane and returning towards ground antenna.
• Ultrasound signal impinging on fetus and returning towards detector.
• Cell phone wave from tower traveling a half mile to user's phone.
• Starlight passing through interstellar dust.
• Underwater song of a whale passing through 6 miles of ocean water.
• Ultrasonic clicks from a bat impinging on a moth and reflecting towards the bat.
• Oscillations in exterior temperature working their way into the interior of an unheated structure.
• Oscillation of the suspension system of a truck causing oscillations in the structure of a bridge supporting the truck.
• Oscillations in ocean levels caused by tides working their way 60 miles up a river estuary.
• Oscillations in AC power voltage driving AC current in a reactive load, such as motors or fluorescent lights.

---

NEXT: More on complex phasors. LAST: More on complex numbers.

---

©P. Ceperley, 2007.

Links for complex phasors

• Wikipedia
• An illustrated explanation.
• From Answer.com
• Circuit theory basics.