Mathematical definition of Fourier series

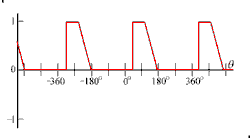
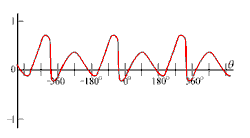
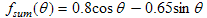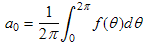Typical waveforms analyzed by Fourier series

Fourier series are used to decompose repeating mathematical functions (such as those shown below) into sums of sinusoidal functions, i.e. to tease the various sinusoidal frequencies out of a waveform.  

a. Balanced square wave function with period of 2π or 360 degrees.	b. Periodic function with sharp corners.	c. Smooth (and a little crazy) periodic function.

Two flavors of Fourier Series

There are a number of "flavors" of Fourier series. In this posting, we give the mathematical definition of Fourier series for the flavor that uses sines and cosines because it does not use complex math and thus may be a little easier to understand. Conceptually, the simplest sinusoidal form would be a series of only cosine (or only sine) terms with adjustable amplitude and phase, such as: 

          .   (1)

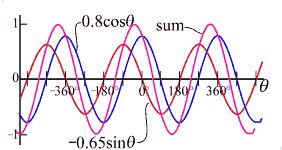
We will eventually get back to this form, but for now we will instead consider another similar form which is easier to mathematically compute.  This form uses both sine and cosine terms with adjustable amplitudes, but the phases are all fixed at zero:

           .   (2)

Equivalence of these two flavors:

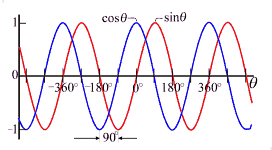
Looking at the figure below (a), we see that sine and cosine functions are identical except that they are phased 90 degrees apart, i.e.  Having both sines and cosines in the series effectively gives us the same flexibility to fit an arbitrary repeating function as does the form (1) that has only cosine terms but with adjustable phases.  To understand this, consider the following various extremes.

• With the b's in (2) set to zero, Equation (2) is the same as Equation (1) with the φ's at zero.
• Instead, with the a's in (2) set to zero, Equation (2) will be equivalent to (1) with the φ's at −90° remembering that  .
• A mix of both the a's and b's gives  φ's at somewhere between 0 and −90°.
• Use of negative a's and/or b's allows us to duplicate (1) with φ's of any angle.

This summing process of sinusoids and use of phasors is shown below and also discussed at length in an earlier posting.  We will discuss this mathematically in the next posting.

a. Sine and cosine functions showing the 90 degrees phase difference between the two.	b. Example of an addition of a sine and cosine function multiplied by coefficients. In this example the sine function is multiplied by −0.3 . At each angle, the purple function labeled "sum" is the sum of the two other functions at the same angle:	c. The phasor diagram for the summing process shown in b, at the left.

Functions of distance or time

In the above equations, we use θ as our independent variable because the argument of sine and cosine functions must be an angle and this variable emphasizes this.  It also emphasizes that the function repeats itself every 2π radians or 360 degrees as is appropriate for Fourier series.   In most applications, we substitute either the product κx or the product ωt  in for θ depending on whether we are working with a function that varies with distance or one that varies with time, where the angular frequency ω = 2πf  (radians per second),  the wavenumber κ=2π/λ (radians per meter),   f  is the frequency (Hz or cycles per second), and λ is the wavelength (meters).   In the case of a propagating wave, the function f usually varies with both time and distance and we use some combination of all the above variables.   In the table below we summarize these variables.

Sinusoidal functions of time. θ = ωt . angular frequency, ω = 2πf  . units for ω are radians per second. f is frequency, with units of Hz or cycles per second. T in the graphs above is the period or length of one complete cycle in seconds. f = 1/T  and   ω = 2πf =  2π/T .

Sinusoidal functions of distance θ = κx . wavenumber, κ = 2π/λ . units for κ are radians per meter. κ is the equivalent to ω for sinusoidal variation in space instead of time. λ is the wavelength, the distance of one complete cycle in meters.

Equations for the coefficients

The next task is deciding how to arrive at the proper amplitudes of the various sine and cosine terms in Equation (2).  In Equation (2), these amplitudes are labeled as coefficients a_{0 ,}  a_n , and b_n .  Explained in more detail, they are:

1. A constant term a₀.  This represents the average value of f(θ).  It can be found by using the standard integral method for finding the average value of a function; that is, we integrate f(θ) over one of its repeating lengths (which happens to correspond to θ varying from 0 to 2π) and divide by the integration length of  2π:
             .          (3)


2. Coefficients of the cosine terms, a_n .  Because of a trick or property, called orthogonality (of the sine and cosine functions used in (1)),  we can calculate the a_n using the relatively simple formula:
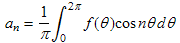           .    (4)


3. Coefficients of the sine terms, b_n .  Using orthogonality again, we can use the similar formula for b_n:
           .    (5)

In succeeding postings I will explain the orthogonality condition and use it to derive Equations (4) and (5). For now, I will simply demonstrate how to use these equations.

An example

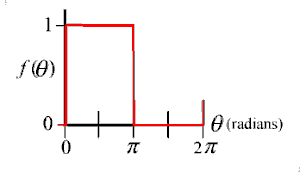
Square wave used in this example.  It is assumed to repeat this pattern every 2π radians.

Suppose we have the repeating function shown at the right.  We show only one cycle, but it is assumed that this cycle continues to repeat.  This function is similar to the very first function (just after the animation) shown in this posting, with the difference being that it jumps between 0 and 1, instead of between −1 and +1 as the above function does.  We use this function as a starting example because it is particularly easy to integrate.  We also have the horizontal axis laid our in radians instead of degrees (2π radians equals 360 degrees).  

We now evaluate Equations (3), (4) and (5).  Starting with (3) to compute the average value of the function, we have:

   
    

So the average value is one half, which we could have surmised by inspection of the figure at right.

Now to do Equation (4).  We have:

   
    

remembering that n is a positive integer and sine functions are zero at multiples of  π.  Someone experienced with Fourier transforms could have predicted this (that all the cosine coefficients would be zero) based on the odd symmetry of the function around the point θ = 0 (after subtracting off the average value).  We will discuss symmetry in an up coming posting.

Now on to Equation (5):

   
    

n bn 1 0.637 3 0.212 5 0.127 7 0.091 9 0.071 11 0.058
The sine coefficients for the square wave shown above, in decimal values and in a bar graph.  Only the coefficient values for odd n's are shown.  The coefficients for the even values of n are zero.  The cosine coefficients are also zero.  The coefficient for the average value, a0 is 1/2.  The line spectrum graph of the square wave is shown on the right where ω is in units of cycles per radian (radians from the horizontal axis above).

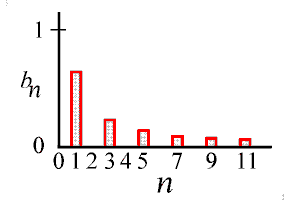
Thus, the sine coefficients are zero for even n's (2, 4, 6, 8, ... ) and equal to 2/nπ for odd n's (1, 3, 5, 7, ... ). Symmetry would have also told us to expect these zero terms.  We have plotted these values at the right.

We could consider the bar graph a spectrum of the square wave, even though the square wave was not given to us as a function of time, or even distance, so the result might be a little unconventional.  We might label the horizontal axis in frequency, if we consider the fundamental frequency of the square wave as 1 cycle per 2π radians =  0.159 cycles per radian.  This I have done at the far right.

Finally, we need to remember that the spectrum shown at the right only shows us the amplitudes of the various sine terms of Equation (2).  The complete split up form of the square wave of this example is a series of sine functions with these amplitudes, as is shown in the animation at the start of this posting.

Copyright P. Ceperley 2009

LAST POSTING: The spectrum of a waveform - Fourier Analysis

NEXT POSTING: Sines, cosines, and phases