| All postings by author | previous: 2.6 Power loss in resonators | up: Simple resonators - Contents | next: 2.8 Valid method of multiplying phasors |
2.7 Energy and power in a resonator by complex methods

In this section we use complex methods to derive the energy and power loss as a function of time. It gives us a chance to see complex methods in action and their advantages and disadvantages over the real sinusoidal methods of the previous sections.
We have included a very short tutorial on complex methods as applied to energy and power at the bottom of this posting.
| Table 1. Derivation of -dU/dt in a shock excited LRC resonator using complex methods. | |
|---|---|
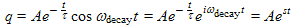 (1a)
(1a)
| We start with the decaying oscillating charge in the LRC resonator and convert it to complex form, as we did in Section 2.2, Equation (6c). |
 (1b)
(1b)
| This is the definition of s in the Equation (1a) above. We also used it in Section 2.1 . |
 (1c)
(1c)
| This is just the complex form of the oscillating current through the circuit, from Section 2.1, Equation (6e). |
 (1d)
(1d)
| Complex phasors generally produce erroneous results when we try to multiply two phasors together. However there is a standard, proven method for finding the average of a squared phasor, averaged over a cycle of the oscillation. The equation is average = ½(x·x) , where x is the complex phasor of interest and x is its complex conjugate. We use this here to find the energy in the LRC circuit resonator. Note that we get a time dependent form, but the high frequency wobble of the previous result has been averaged out. |
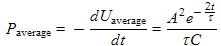 (1e)
(1e)
| Here we take the simple time derivative of Equation (1d) above. |
 (1f)
(1f)
| We repeat the method discussed for Equation (1d) above to calculate I2R averaged over a cycle of the phasor oscillation. The result is time dependent, but the highest frequency dependence has been averaged out. |
We now compare the results in Equations (1d), (1e), and (1f) with the results obtained by real sinusoidal methods in the previous two sections. These previous results are listed in Equations (1a), (1b), and (1c) of Section 2.6. We see that the results above in our current section agree with the slowly varying part of the previous results, i.e. the factor in front of the high frequency parts.
| Comparison of complex and real methods for power computation | |
|---|---|
| Advantage of complex methods: | Computational simplicity. We see this simplicity by comparing the multiple steps of the previous two sections using real sinusoids with the very brief complex derivation above. |
| Disadvantage of complex methods: | High frequency time dependence is averaged out. |

Tutorial
| Short tutorial on standard methods of calculating power using complex phasors |
|---|
|
If you should be interested, there is a discussion of complex phasors in general at an earlier posting. Problem with multiplying two phasors togetherComplex phasors must be used with care when calculating energy, power, or any quantity that involves multiplying two oscillating parameters, i.e. phasors, together. We have mentioned this before under limitations of complex method. To illustrate the problem of multiplying two phasors together we offer the following typical example. Suppose we try to calculate I2R by squaring the complex phasor of I, multiplying by R and taking the real part, as we might for a normal phasor calculation:
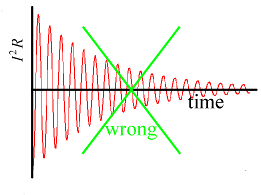
Below in Figure 1b we graph these results. Figure 1a is a repeat of a graph of the previous section showing I2R calculated with real sinusoids which is how the real LRC circuit would behave. Note that Figure 1b shows I2R to be oscillating positive and negative, even though squaring I should insure that I2R will always be positive. Equation (2a) and Figure 1b are incorrect. Standard methodThere is no good standard way to calculate the instantaneous behavior of I2R using complex phasors. However there is a well established complex method for calculating the average of the product of two phasors, such as I and V. The formula is: where V stands for the complex conjugate of the oscillating voltage V. As we noted before, the averaging is a moving-average taken over a phasor cycle. The result of this average can be time varying itself, but does not contain the rapid oscillations of the phasors of I and V. To understand Equation (2b) we represent I and V in polar form as I = I0eiφ1 eiωt and V = V0e−iφ2 e−iωt , where φ1 and φ2 are the polar (phase) angles of the constant (non-rotor) parts of I and V. Now the right side of Equation (2b) becomes ½ Re(I·V) = ½ Re(I0eiφ1 eiωt V0e−iφ2 e−iωt) = ½ I0V0Re[ei(φ1−φ2)] = ½ I0V0cos(φ1−φ2) . This final expression is correct for the power, averaged over one cycle of the phasors (i.e. of the complex rotors) involved. Squaring a phasorIn the case of squaring a phasor, such as in calculating I2R, we simply replace the V with a IR as we did in Equation (1f) above. Because the R is a real constant, R = R and also it can be taken through the Re() operator at will. In this case ½Re(I2R) (with a real R, i.e. pure resistance) we get ½Re(I·IR) = ½|I|2R because any complex quantity times its complex conjugate equals its magnitude squared. If instead of a real load, i.e. R, we had a complex load, ZL (composed for resistors, capacitors, and/or inductors) the load ZL needs to be considered more carefully. In this case we get ½Re(I·IZL) = ½|I|2Re(ZL) . We used the fact that Re(ZL) = Re(ZL) . If we instead wanted to evaluate the average power using the equation P = V2/ZL (for parallel elements) using the above methods, we would do so as: Paverage = ½Re[V·(V/ZL) = ½|V|2Re(1/ZL) ] = ½ (|V|2/|ZL|2) Re(ZL). Note that Re(1/ZL) does not equal 1/Re(ZL) but instead is given by Re(1/ZL) = Re(ZL)/|ZL|2 . Complex average powerOccasionally you will see the complex (average) power calculated without the Re(...) operator, as: This equation is used primarily when you have a source of power that is located in one place driving a device (or power-using circuit called a load) located in another place or region and the two regions are connected by wires. It is not particularly useful for our study of resonators, at least for their impulse response, but we include it for completeness. The real part of Equation (2c) is the average net power absorbed by a load, while the imaginary part is the amplitude of the reactive power that flows in and out of the load each cycle of the phasors. Be warned that both parts of this result mask the pulsing nature of these quantities. In reality the absorbed power looks more like the red line in Figure 1a below (i.e. pulsating), while the real part of the Equation (2c) looks like the blue line (smoothly varying). The reactive power calculated using Equation (2c) also looks like the blue line in Figure 1a (smoothly varying), while in reality the reactive power will have a time dependence like that in Figure 1b (oscillating). People that use these quantities need to remember these weaknesses of Equation (2c) and compensate accordingly. This warning about masking the pulsating nature of the power also holds for all the other averaging equations in this tutorial as well. |

|
|

|
| Figure 1a. The instantaneous power calculated in the previous section, Equation (2e), using real sines and cosines. | Figure 1b. The incorrect power calculated by incorrectly using complex phasors. |
P. Ceperley Feb. 2010
| All postings by author | previous: 2.6 Power loss in resonators | up: Simple resonators - Contents | next: 2.8 Valid method of multiplying phasors |


