| All postings by author | previous: 2.2 Complex math derivation | up: Simple resonators - Contents | next: 2.4 How a resonator works |
Simple Resonators - Shock excitation
2.3 Strong damping - critical dampingFor some applications, oscillations in resonant structures are not desirable. For example, shock absorbers in automobiles are designed to dampen out oscillations of the suspension, while still allowing the suspension to be responsive to bumps in the road. Damping is also required for engine and motor mounts, body panels and other parts of cars and aircraft, and read/write arms in computer hard drives. These parts all have the ingredients of a mass-and-spring resonator: a mass, a spring, and damping. Therefore the equations of the previous section are appropriate, if converted to general coefficients, such as were used in Table 6 on a previous posting. Table 7 below uses general coefficients and derives the frequency and decay constant for three damping strengths: underdamping, critical damping, and overdamping. Note that these terms are usually used in connection with applications designed to prevent oscillations and not with normal resonators in which oscillations are desirable as discussed in previous sections.
Note also that changing the damping in a mechanical resonator such as that in the animation involves changing something mechanical. For example, in the animation, adding damping might involve putting cotton filling or porous sponge material inside the rubber tire that supports the platform. The air flow through this material would absorb energy as the tire is distorted by the weight of the girl. A more effective method would be to use a separate air chamber, such as that inside the middle of an inflated inner tube and provide a hole in it to let air to pass from the outside atmosphere to inside this chamber and back the other way as the girl compresses the tire. By changing the hole size and thus the resistance to air flow, one could change the damping.
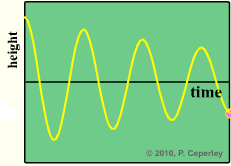
The animation above illustrates the effect of different values of the damping coefficient on the resulting "oscillations". Mouse over it (or click on it) to set it into motion. Select the type of damping you wish to observe. A little experimentation with the animation will convince you that critical damping leads to the fastest reaching of stationary equilibrium. Overdamping has a nice exponential decay with no oscillations, but it causes a slower decay than with critical damping. Underdamping causes over shooting, oscillations, and a slower reaching of stationary equilibrium. Of course, the exact values of the damping coefficients affect the speed at which equilibrium is reached, but coefficients adjusted for critical damping result in the fastest equilibrium.
Two more notes before we start the math:
- Real shock absorbers as well as some other dampers in modern technology use more sophisticated methods than addressed in this posting, such as damping only in one direction of motion, or computer controlled damping.
- Most of these posts in this series are directed towards applications that require oscillations to work and would be considered to be extremely "under damped" in the language of this particular posting. This particular post is odd in that it is directed towards applications requiring abatement of oscillations. We include it for completeness.
| Table 7. Equations for a heavily damped resonator | |||||||||||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
 (7a)
(7a)
| We repeat the general second order differential equation, last shown in Equation (6a) (of section 2.1) with general coefficients A, B, and C. In this case C is not the capacitance, but instead just the last coefficient in this general equation. | ||||||||||||||||||||
 (7b)
(7b)
| Here we use the complex equation, Equation (6h), from the last posting that gives exponential coefficient, s. We have substituted R = 2L/τ (5a) and LC = 1/ω02 (5c) to converted it to the general coefficients as used in Equation (7a). | ||||||||||||||||||||
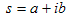 (7c)
(7c)
| Here we break up s into real and imaginary parts. a is the real part of s, i.e. Re(s), and b is the imaginary part of s, i.e. Im(s). | ||||||||||||||||||||
 (7d)
(7d)
|
When we insert s in the form of (7c) into a typical damped oscillating parameter, such as y(t) = Aest, similar to the q(t) in Equation (6c), we get (7d). Looking at the extreme right of (7d), we see that eat is an exponential growth factor (for positive a's) or exponential decay factor (for negative a's). The eibt factor has a complex argument meaning that its real equivalent is a sinusoid.
The A in this equation and also in the equations that follow is not the constant in Equation (7a) above. Instead the A as used here (and below) is the initial amplitude of oscillations. Also, as per the standard convention with complex phasors, we take only the real part of Equation (7d) for Equation (7e). | ||||||||||||||||||||
 (7e)
(7e)
| This is the real part of (7d). Comparing (7e) with (6b) of the previous posting, we see a is the damping coefficient (i.e. −1/τdecay), and b is the angular frequency (i.e. ωdecay). That is to say Re(s) = a = -1/τdecay and Im(s) = b = ωdecay . | ||||||||||||||||||||
|
τdecay = −1/a = −1/Re(s) (7f) &omegadecay = b = Im(s) (7g) y(t) = Aet/τdecay cos ωdecayt (7h) | Here we summarize the above. | ||||||||||||||||||||
When we have strong damping, the equation under the square root sign of (7b) (the discriminant) can be positive, zero, or negative which greatly affects the resulting "oscillations". These three cases are called underdamped, critically damped, and overdamped, respectively. This is summarized as:
We work out the solutions to the "oscillations" for these cases next: | |||||||||||||||||||||
| |||||||||||||||||||||
 (7b)
(7b) (7i)
(7i) (7j)
(7j)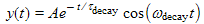 (7k)
(7k)
|
The underdamped case where τ > 1/ω0 and the discriminant in (7b) is positive, i.e. ω02 − 1/τ2 > 0. This is basically the same case as we have been discussing in all the previous postings where we have nice oscillations. The oscillations of the parameter are as given by (7k). We see these decaying oscillations in Fig. 1a above. We have repeated Equation (7b) at the left (as well as for the next two cases below) because it is central to understanding the behavior of the resonator.
| ||||||||||||||||||||
 (7b)
(7b) (7l)
(7l)
|
The critically damped case where τ = 1/ω0 and the discriminant in (7b) is zero , i.e. ω02 − 1/τ2 = 0.
This means that ωdecay = Im(s) = 0 and oscillations do not occur.
The real part of s is still present and from (7b) is given by τdecay = −1/Re(s) = τ . All "oscillating" parameters do not oscillate, but instead simply decay as given by (7l) and seen above in Fig. 1b.
| ||||||||||||||||||||
 (7b)
(7b) (7m)
(7m) (7n)
(7n) (7o)
(7o) |
The overdamped case where τ < 1/ω0 and the discriminant in (7b) is negative , i.e. ω02 − 1/τ2 < 0. This means that the square root term in (7b) has another √−1 = i in front of it. Multiplying that i with the one already in (7b) we get an entirely real term and no imaginary term.
Therefore by (7g) ωdecay = Im(s) = 0 and the parameter y(t) in (7h) does not oscillate as we see above in Fig 1c.
We have a situation much like that in the critical damping case, only exponential decay as given by (7m). However, in this case, the now real square root term adds to the real 1/τ in (7b) making the decay time longer than in the critical damping case, shown in (7n) and (7o). Note: the real part of s determines the damping as per (7i). One confusing aspect of overdamping is that τ is no longer the operational decay time as it was in the underdamping and critical damping cases (where τ = τdecay). Instead, in the overdamped case we must consider τ to be just a collection of constants as shown in the table below, while the operational decay constant in the exponent in (7m) is the larger τdecay given by (7o).
The answer is: shortening τ involves adding more resistance to the damping term in the differential equation, i.e. making R larger in the LRC circuit or in the mass-and-spring resonator. A larger R, in addition to adding dissipation, also adds resistance to any current flow or motion for the two resonators. This added resistance actually slows down the settling to equilibrium once we have enough resistance and dissipation to kill the oscillations. Overdamping is just what its name implies: over doing the damping. | ||||||||||||||||||||
P. Ceperley, Jan. 2010.
| All postings by author | previous: 2.2 Complex math derivation | up: Contents - simple resonators | next: 2.4 How a resonator works |