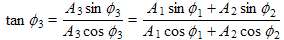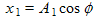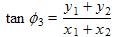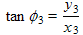A graphical method that helps in the understanding waves and oscillations, and also helps with calculations, such as wave addition, is called "phasor diagram". Sadly enough, this has nothing to do with Star Trek or the "phasor" weapons used in science fiction movies, although phasor diagrams would undoubtably used in their design when that time should come, since phasor diagrams play a central role in the of understanding of lasers.
The oscillations and vibrations really only involve motion along one direction or with regard to one parmameter, however in this method we artificially add a second dimension just for the sake of understanding. We imagine a rigid rotor or vector moving around in circles around the origin, as illustrated in the diagram to the right. It is constructed so that the projection or shadow of the tip of the vector moves back and forth exactly like the oscillation we are studying. The angle that the vector makes will the x-axis is made equal to ωt + ϕ. Because of the t, or time, factor that increases as time increases, the angle will constantly increase, making the vector rotate at a constant velocity. The projection that the vector makes on the horizontal or x-axis will be
x = r cos (ωt + ϕ),
so that this process does give us the cosine wavefunction in the end. The angle ϕ is the angle the vector make with the x-axis initially, i.e. at time t = 0.
Phasor diagrams are similar to an analog clock face. In such a clock face we use the rotating hands to keep track of time. Time, however, has nothing rotating or circular about it. To the average man or woman who is not an astronomer, time is a one dimensional progression, more like a time line. Of course time also has a repeating nature to it, like a time line that keeps replaying. But, for mechanical convenience, we use a circular clock face to keep track of time, because repeating motions are easiest to construct with rotating circular devices. Similarly, for computational ease we will use these circular phasors to track oscillations and waves, because these diagrams make computational manipulations of oscillations and waves easier.
To better understand this, study the animation below.
Presented with a real oscillation to simulate, such as AC power or the pressure oscillations in a musical note, the phasor method instructs us to imagine a rotating vector, whose projection (or shadow) is the observed oscillation. The oscillation shown here has an amplitude of 1, i.e. r = 1. Of course, we can change the vector length for any amplitude. It is perhaps more common to make the projection (or shadow) on the x-axis as is shown in the previous diagram, instead of below the circle as is shown in this animation. This animation can be downloaded free at George Mason University Archival Repository. Please read the fair use policy for this work.
Another phasor animation:
Mouse over the image to see the action. When the animation is finished, mouse off and on again to replay it. Press − in the +/− button to hid the cartoon features of this animation and + to restore them. This animation can be downloaded free at George Mason University Archival Repository. Please read the fair use policy for this work.
Adding two waves in a phasor diagram
Ok, a phasor diagram is suppose to make it easier to add waves. But, exactly how is that done?
Someone who is very familiar with vector addition may have recognized the equations we laboriously derived for adding cosine waves above. I'll repeat them here:
 and
and

Notice that all the terms are of the form A1cosϕ or A1sinϕ . These are just the x and y components (or projections) of the vector A1 plotted on the phasor diagram to the right. Note that the bold symbol A3 stands for the whole vector, while the italized A3 stands only for its amplitude. That is to say:
and
making our equations become:

These are just the equations for adding two vectors: we add their x components together to find the x component of the sum, call it x3, and add their two y components to find the y component of the sum, called y3. Then the magnitude and tangent of the angle of this the sum vector should be (as we have):
Thus if we add two phasor vectors together, we will get the phasor vector for the correct wavefunction according to the complicated cosine addition formulas.
Below we have an animation for the process of adding two oscillations using phasor diagrams. We use the oscillations of two people on the ends of bungy cords, however the oscillations could also be the oscillations of electrical voltages in AC power or the oscillations of the air pressure as a sound wave passes through. Read the caption below the animation for details on it.
Click on "together" to see the action. When the animation is finished, click on this or other buttons to see this or related animations. Move the mouse off the animation to suspend it and back on to restart it.
The "together" animation shows the pair oscillating in unison or "in phase" with a phase difference of 0 degrees. The gray sum vector represents the sum of the two oscillations and for zero phase difference has an amplitude equal to the sum of the amplitudes of the two people. Zero phase difference results in the largest possible sum oscillations.
One use of summing the two oscillations is to find the motion of the center of mass of the man and woman. The center of mass motion is simply the sum of the motions divided by two. It is shown as a green cross and moves up and down with the motion.
The "in opposition" button delays the release of the woman to put the pair oscillating with 180 degree phase shift between them, or in opposition with each other. When the man is down, the woman is up, etc. This phase results in a sum amplitude equal to the difference between the two amplitudes. In this case the sum is the smallest possible for all possible phases. Note that the center of mass hardly oscillates at all. If the oscillations of the two people were of exactly the same amplitude, then the sum, as well, as the center of mass oscillations would have zero amplitude in this case of 180 degrees phase difference. That is to say that with 180 degree phase difference the two oscillations would cancel in a summing process or would destructively interfere.
You should compare the relative directions of the phasor arrows in the two cases (after the woman has been released. In the first case, with 0 degrees phase shift, the arrows are together, cause the maximum possible sum. In the second case, the arrows are spaced 180 degrees apart, causing the minimum possible sum.
The "random phase" button delays the woman's release a variable amount so that a different phase shift will occur each time this button is clicked. The resulting sum oscillation is the vector sum of the man's and woman's phasors. The summing parallelogram is seen in light gray in the phasor diagram to the left. The sum oscillations have an amplitude some where between the amplitudes of the two extremes cases, that of 0 and that of 180 degree phase difference. In general there will be a phase difference between the sum and either person's oscillations.
The "difference" button shows the difference between the man's and woman's oscillations. One application for a difference is to calculate the distance between the two people as a function of time. We illustrate this length by the length of the blue ribbon stretched between their hands. You can see that its length varies in an oscillatory fashion. This button also adds a random phase shift between the man's and woman's oscillations.
Press − in the +/− button to hid the cartoon features of this animation and + to restore them. This animation can be downloaded free at George Mason University Archival Repository. Please read the fair use policy for this work.
All the above "buttons" show cases in which the frequency of the two oscillations are the same. However the phasor method also works for adding or subtracting oscillations of differing frequencies. We show this next:
Click on either button to see the action. Mousing over the other button can be used to speed up or slow down the action without restarting it. Mouse off the animation to suspend it and mouse on to continue it. Click on a button to restart it. Clicking will restart the action whether or not it has finished. Each time the action is restarted, a new frequency difference will be used, changing the rate of beating. In these animations, we neglect damping, which will normally reduce the oscillations as time goes by. We will discuss damping in future lessons.
We needed to compress the horizontal axis to show many more oscillations than in the previous animation in order to be able to see the beating phenomena. Press − in the +/− button to hid the cartoon features of this animation and + to restore them. This animation can be downloaded free at George Mason University Archival Repository. Please read the fair use policy for this work.
Options:
- If you are having trouble with your flash player, you can see
- a still image by clicking here
- or a animated gif file (2.5MB) of part of the action by clicking here.
- To hear examples of acoustical beating, click on the captions below the following flute players.
Why do phasor diagrams work?
We have already answered this above, at least in part, but it is an important point that could stand repeating and further refinement. Our answer:- Most simple oscillations, ones having a "linear" restoring force, can be mathematically represented with cosine (or sine) functions, for example: y(t) = A cos(ωt + ϕ).
- This is a result of the type differential equations that these oscillating systems are constrained to follow and has nothing to do with circular motion.
- It just so happens that a cosine function is also, independently of oscillating phenomena, the projection of a vector rotating at constant angular speed around the origin.
- Thus, if we should want, we could choose to have the projection of a rotating vector represent an oscillation. This would have the handy feature that the argument of cosine function in the oscillation which has units of radians, now can be represented as an actual physical angle.
- If we have two vectors rotating around the origin, then their sum vector will also rotate around the origin. This sum vector will have an x-component equal to the sum of the x-components of the two original vectors. Thus the projection of the sum vector is the sum of the two oscillations.
- Whereas there was no simple illustration for adding two cosine functions, with the phasor method there is a simple graphical method for adding two rotating vectors.
- So, given oscillations to add and subtract, we construct the required rotating vectors, called a phasor diagram, and graphically add and calculate the resulting sum and/or difference oscillation.
NEXT: More on Complex Numbers.
© P. Ceperley, 2007.