
| All postings by author | previous: 3.19 Applying methods of 3.18 to the circuit of 3.17 | up: Contents | next: 3.21 Reflection and absorption coefficients for transmission lines with loads |
This posting includes flash animations showing the physics discussed. Most computers have a flash player already installed, but if yours does not, download the free Adobe flash player here.
|
3.20 Derivation of wave properties for transmission lines
Keywords: transmission line, telegrapher's equation, types of transmission lines, equivalent circuit, wave solution, propagation constant, characteristic impedance, wave energy, wave power, flash animation
Topics covered in this posting
- Transmission lines are widely used in communication technology. We discuss the the various kinds of transmission lines and derive the basic equations for wave propagation on these.
- Much of the behavior of waves on a transmission line is captured by the propagation constant and characteristic impedance of the transmission line.
- We derive equations for these.
- We discuss energy and power of the waves on transmission lines.
Contents of this posting
| 1. Derivation of telegrapher's equations | ||||
|---|---|---|---|---|
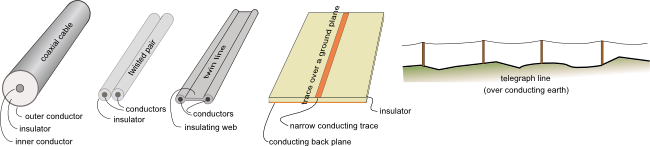
This posting is meant to be a summary of the rationale behind the wave equations for transmission lines. It also includes discussions of some of the properties of the waves based on the wave equation. A transmission line consists of a pair of conductors that are uniform in cross section over an extended length and separated by a likewise uniform insulator. Fig. 1 shows several standard transmission lines. More are discussed in this reference and here. Also, much of the equations for transmission lines can be applied, with some restrictions, to plane wave propagation through a uniform medium and to wave propagation through waveguides and optical fibers. In this posting we will focus on waves in traditional transmission lines. The standard transmission line can be electrically modeled by the circuit shown in Fig. 2, where the L-R-C-G unit cell is repeated many, many times down the length of the transmission line. We consider the case where the unit cell is very short compared to the wavelengths we will investigate. That is
ℓ << λ . (1) We now write two differential equations governing the voltage and current along the transmission line:where ΔV is the voltage drop across one unit cell of the circuit in Fig. 2, i.e. across an L R combination of a cell. The current I of a cell is the current passing through L and R of a cell. The change in current ΔI is the change in current from one unit cell to the next due to current being drained off by the conductance G between the conductor and ground and by the capacitor if the voltage across it is changing, i.e. it is being charged or discharged. For the component values L, R, C, and G, we substitute the values per unit length for the transmission line times the length of a cell. That is, for L we substitute L1ℓ, the inductance per length times the length of our unit cell. Using component values per unit length makes more sense for the uniform pair of conductors. The equations for the component values per unit length for some standard transmission lines can be derived using standard electromagnetic theory (see this reference - towards its end). Note that R1 is the resistance per unit length of the conductors and G1 is the leakage conductance between the conductors (also per unit length). Both R1 and G1 cause signal loss (attenuation) in real transmission lines. Sluggishness in dielectric response [2nd ref] of the electrical insulators in transmission lines is also a common cause of loss, but can be considered a frequency dependent component of G1 for the sake of calculation. We change ℓ into Δx and divide both equations of (3) by Δx: Finally, we take the limit of very small ℓ's, i.e. very small Δx's, in which the Δ's are replaced by partial differentials: The equations in (5) are known as the telegrapher's equations and were developed by Oliver Heaviside in the 1880's to describe the electrical properties of long distance telegraph lines which were the developing new technology of the day. 
The two equations in (5) can be combined to eliminate I and yield a wave equation:
With some rearrangement, this can also be expressed as: |
| 2. Lossless solutions to the wave equation |
|---|

If the loss elements, R1 and G1, are both zero, then this equation becomes simple: which has solutions of the form: where A and B are complex constants representing the complex amplitude (amplitude and phase shift) of the positive and negative going sinusoidal traveling waves. ω is the angular frequency (radians per second) of the wave and κ is the wavenumber (radians per meter). They are related to the velocity c of the wave by: We can also solve for the characteristic impedance of the transmission line. The characteristic impedance is defined as the ratio of the voltage in a traveling wave propagating in only one direction to the current in the same wave. We start with the left equation of (5) with R1 = 0 and substitute either the first or second term (either the positive or negative going traveling wave) of (8) into it: 
where we have also assumed that the current I has the same form as does the voltage, i.e. I = Aei(ωt ∓ κx) . The minus sign in (10) is to be used for positive going traveling waves while the plus sign is for negative going traveling waves. Using (9) along with (10) we can calculate the characteristic impedance Z0: where the + sign is used for positive going traveling waves and the minus sign for negatively going traveling waves. For more about simple waves like this, see an earlier posting. |
| 3. Wave solutions with loss | ||||||||
|---|---|---|---|---|---|---|---|---|
|
If R1 and/or G1 is not zero, then the equations are messier and it is useful to start off assuming a sinusoidal solution. Conventionally one picks a general solution of the form: 
where γ is the propagation constant. Note that there is no complex constant i before the γ in the exponent of (12). We next substitute (12) into (6) and cancel the factors common to all terms. This yields: This can be rearranged and solved for γ : where α and β are defined to be the real and imaginary parts of the propagation constant γ . We can understand the roles α and β play by substituting the first part of (14) back into (12): We see from the last part of (15) that α occurs in the factor e−αx which modifies the amplitude A making the effective amplitude of the wave become smaller as it propagates. For this reason α is known as the attenuation constant (units are 1/meters or nepers/m where neper is a "dimensionless unit", similar to radians). The second constant β serves the same role as did the wavenumber κ in (8) and governs the wavelength, i.e. λ = 2π/β . β is known as the phase constant with units of radians per meter. Note that the ± sign in front of the square root in (14) allows for both positive or negative going waves. The + sign is used with positive going waves and makes (15) have positive values of α and β. This results in the waves being attenuated more and more for larger x value as we would expect and also results in sinusoidal functions that move in the direction of positive x as time increases (with attenuation). When we use the minus sign in (14) we get negative values of α and β which cause more attenuation as one goes in the negative x direction, and the sinusoids will move in the negative x direction as time progresses.
To calculate the characteristic impedance as we did in section 2 above, we substitute (12) into the first equation of (5): We solve for V / I to give us:
Again we see the ± sign in the equation. Because the ± sign came from (14) we interpret its use as we did for (14). That is, the plus sign is to be used for positive going waves while the minus sign is for negative going waves. | ||||||||
| 4. Allowed ranges of the arguments of the propagation constant and characteristic impedance | ||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|
|
We next investigate the allowed ranges of the complex arguments of γ and Z0 . We rewrite (14) and (17) in terms of the series impedance elements and the parallel admittance elements (for positive going waves): 
where we define the series impedance and parallel admittance as: Because all four of the component values (R1, L1, G1, and C1) are real and positive (except in really odd environments like an active gain area of a laser), the values of Zs and Yp are restricted to the first quadrant of the complex plane, i.e. positive real and imaginary parts. That is to say that if we express Zs and Yp in polar form:
then the arguments of both Zs and Yp will be in the range of 0 to π/2 radians. Then (18) means that the arguments in (20) will be given by:
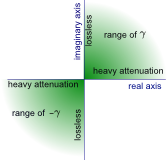
Equation (21) indicates that the argument of γ is the average of the arguments of the series impedance and the parallel admittance. The argument of Z0 is half the difference between the arguments of the series impedance and the parallel admittance. This means that arg(γ) being an average will be in the range of 0 to π/2 radians, while arg(Z0) will be in the range of −π/4 to +π/4 . Below in Fig. 4 we show these ranges graphically. Negative going waves have a minus sign in front of both equations in (18). This will have the effect of inverting both γ and Z0. This will mean that for negative going waves arg(γ) will range from −π to −π/2 radians while arg(Z0) will range from 3π/4 to −3π/4 radians (centered around π radians).
| ||||||||||||
| 5. Energy and power in waves | ||||||||
|---|---|---|---|---|---|---|---|---|
|
In a transmission line the energy in a wave is stored in both the inductance and capacitance of the line. The total energy stored in both per unit length of the transmission line is given by: for real functions (sinusoidal) of the voltage V and current I. For complex forms of the voltage and current, we use:
We cannot use |V|2 or V⋅V* where V* is the complex conjugate of V because that would give the time averaged power. We want the time varying power. This issue is discussed in this posting. The power transmitted along the line is given by:

where the first form above is appropriate for real (sinusoidal) forms of I and V. The power dissipated per unit length by the transmission line is given by:
where the first form above is appropriate for real sinusoidal forms of I and V. With all the equations (22) - (25) above we could use the relation between I and V expressed in equation (11) to eliminate one of these two variables, if the wave was entirely a traveling wave, entirely a standing wave, or a known constant fraction of the traveling waves in each direction. Below we plot the above energy and powers for various waveforms. The first set of graphs (Fig. 5) is for pure attenuated traveling waves. The second set is animated (mouse over each) and shows these quantities when there is a standing wave added to the traveling wave. The animated graphs below show the complication of a mix of traveling and standing waves. In Fig. 6 we show cases where traveling waves with various attenuations hit a wall and reflect. We will see that depending on the strength of the reflected wave, the energy and power flow is complicated. We will visit this complication mathematically at the end of the next posting.
| ||||||||

| Painting by George M. Ottinger. Displacement of the pony express by the telegraph. |
| All postings by author | previous: 3.19 Applying methods of 3.18 to the circuit of 3.17 | up: Contents | next: 3.21 Reflection and absorption coefficients for transmission lines with loads |




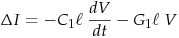




 . (6)
. (6)










 . (17)
. (17)

 , (20)
, (20) . (21)
. (21)




 . (23)
. (23) , (24)
, (24)



