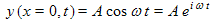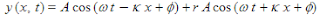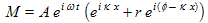Reflection of waves as a process to make standing waves

   In memory of author Hans Christian Andersen and sculptor Edward Eriksen and their The Little Mermaid, Copenhagen, Denmark, 1836 and 1913

Waves usually reflect when they hit any sort of obstruction or change in the media. Sometimes the reflection is total, other times it is partial with the non-reflected waves continuing, being absorbed, or partly continuing and partly being absorbed. Above and below we show animations of the reflection process, as demonstrated with waves on a rope above and with water waves below. Mouse over the animations to start them, off to suspend them, or click on them to restart.

No reflection

We will focus mostly on the animation below which is set up to demonstrate a number of different reflecting conditions and principles. This animation initially starts with "no reflection" active. In this setting, we see a pure traveling wave with no reflection. Some of the features of this wave are:

• There is a pure traveling wave, propagating from left to right, unimpeded.
  
  
• The light gray region around the surface of the wave shows the envelope of the wave. This is the region swept by the wave (i.e. the water surface) as the wave passes. You can see that for this pure traveling wave, the envelope is constant, does not vary with x, and that all points are swept equally as the pure traveling wave passes.
  
  
• The envelope's minimum amplitude equals its maximum amplitude, as indicated by the little "min" and "max" bubbles. This equality is always true for a pure traveling wave with no attenuation.
  
  
• Below the wave, we see the phasors, for various points along the wave. Note that where the wave is maximum, at the wave crests, the phasors are pointing to the right, totally on the real axis, in which direction the real part is maximum. The phasors at the wave troughs are pointing in the opposite direction, to the left, where the real part is negative.
  
  
• The phasors are all of the same length and point at progressively different angles. This is always true for a pure traveling wave (having no attenuation).
  
  
• Along the bottom edge, a little right of center, we see a number for the standing wave ratio. The standing wave ratio is a measure of the amount of standing waves in the system. It is defined as the envelope's maximum amplitude divided by the envelope's minimum amplitude, as indicated by the max and min bubbles. In this case of zero reflection, it equals one since the min equals the max. This value of one is indicated for the standing wave ratio at the bottom edge of the animation. A standing wave ratio of 1 means no standing waves are present, that the waves are purely of the traveling wave type. We will discuss the standing wave ratio more below.
  
  
• The notation in the center of the bottom edge of the animation indicates that the reflection coefficient is zero, meaning that there is no reflection in this case. The angle of the reflection coefficient is indeterminate since there is no reflection. This is indicated by a question mark.

Click here for a copy of the above animation in a separate window that can be sized (even to fill the entire screen) and positioned independently from the text. Your popup blocker may prevent a separate animation from being launched. In some browsers the separate animation will stay on top if you only use your scroll wheel to scroll down this text, and do not click on the text.

Click here for a slightly different version of a separate window. This version allows you to save the animation to a file by clicking on "file" and then "save page as" to get this animation into your computer. Please read the fair use policy.

Total Reflection, no phase shift

If you click "total reflection +", you see a sea cliff appear on the right hand side which will reflect 100% of the waves.

• Wait for the wave to propagate up to the cliff, reflect, and travel back across the screen. At this time you will see the formation of a pure standing wave formed by the 100% reflection of the incident wave. As we saw in the last two postings, a standing wave is the superposition of two equal, but oppositely propagating traveling waves, which is exactly the situation in this case where we have 100% reflection.... all of the incident wave is reflected giving an oppositely propagating traveling wave in addition to the incident wave.
  
  
• In this case, you see that the light gray envelope of the pure standing wave is not constant as it was with the no reflection case, but has well defined peaks called antinodes or maximums, and minimums called nodes or zeroes.
  
  
• The minimums of the envelope of a pure standing wave are zero, i.e. the wave has zero amplitude at the minimums, which is again different from the no reflections case. At these points, there is no vertical motion of the water surface, even though the wave field is very active on either side othe these points.
  
  
• A maximum occurs at the reflecting surface.
  
  
• The standing wave ratio (the max divided by the min) is now equal to infinity, since the denominator, the minimum, is zero.
  
  
• The reflection coefficient is now 1.0 or 100%, and the phase angle of the reflected wave is 0°. This means that the phase of the wave immediately after reflection equals that of the wave immediately before reflection.
  
  
• The phasor pointers, while still rotating, are pointing all in the same direction or at 180° from the rest. Their lengths vary in proportion to the amplitude of the envelope at a particular point. This is quite different from the case of the pure traveling wave we looked at first, where all phasors had the same length but different directions.

Total reflection, 180° phase shift

If we click on "total reflection −" we have a setup where the wave undergoes a 180° phase shift upon reflection.

• Such a phase shift is rather hard to achieve for water waves, but it is a common occurence in some wave systems such as in the case of a sound wave traveling down a tube...an open end of the tube will cause a near-perfect refection with a 180° phase shift. It is also the most common reflection for waves on a string or rope, such as in the mermaid animation at the very start of this posting. Hold the mouse button down on that animation to achieve longer wave trains to more clearly see the standing waves.
  
  
• The envelope, or light gray region, is very similar in shape to what it was with "total reflection +" case, only that the maximums and zeroes are shifted over from before. Now, a zero or node occurs at the point of reflection. We get a zero because the reflecting object causes a 180° phase shift in the wave, so that the reflected wave is 180° out of phase with the incident wave right at the point of reflection and the two waves cancel there.
  
  
• The complicated reflecting barrier shown (in the second animation), as is needed to cause such a phase shift in water, will not have a single flat reflecting surface, but we will consider the effective "reflecting surface" to be at the right hand edge of the animation. A minimum, i.e. zero, occurs at this "reflecting surface".
  
  
• As before, the standing wave ratio is infinite because the minimum is zero giving a zero in the denominator.
  
  
• The reflection coefficient listed on the bottom of the animation is 1.0 with a phase angle of 180°.

Variable refection coefficient

If we click "variable reflection" the animation uses a random number generator to set, at random, the reflection coefficient and the phase angle. If you don't like the values selected, click on it again for a new set of values.

• The reflection coefficient and phase angle selected are shown in the center of the bottom edge of the animation.
  
  
• The envelope will now be somewhere between the three cases above, with minimums and maximums, and where the minimums are not zero.
  
  
• The standing wave ratio (the maximum divided by the minimum) will be some number larger than 1.0 but smaller than infinity. This means we have something between a pure traveling wave and a pure standing wave. We can think of this as a mix of the two: perhaps a standing wave with a extra traveling wave added to it.
  
  
• The phasor pointers vary in length and in the direction they point.
  
  
• These waves are fascinating to watch. The wave field has a traveling wave component that continually travels to the right. At the same time the waves have these envelope minimums to slip through. No matter how tight the minimums are, the waves somehow manage to configure themselves to magically slide through the constrictions.
  
  
• We can click "show components" to see a mathematical dissection of the wave into two pure traveling waves. The red part is a traveling wave propagating to the right and the blue part is a traveling wave propagating to the left. The amplitude of the blue wave will be less than that of the red wave, since only a fraction of the red wave is reflected (the ratio of the two equaling the reflection coefficient.) You can watch how the two wave components slide in opposite directions, making the maximums in the black total wave when their peaks pass each other.
  
  
• I have shown as a reflecting barrier, a messy, wave absorbing, seaweed choked cliff with under seas rocks, as might be expected to produce a reflection coefficient with a partial reflection and complicated phase angle.

Math of reflections

We can mathematically express the "incident" wave, as:

,

where we have shown both the cosine and the imaginary representations.

The "reflected" wave is just this incident wave times the reflection coefficient and shifted in phase by the phase of the reflection coefficient. We also need to change the sign of the wavenumber κ because the reflected wave is traveling in the reverse direction from the incident wave. In addition, it is important just where the reflection takes place. For the moment, we will assume that it takes place at x = 0, placing the x origin on the far right side of the screen and all the wave activity is in the negative x region. The equation for the reflected wave is:

,

where Γ, capital gamma, is the complex reflection coefficient and is defined as Γ=re^iφ where r is the magnitude of the reflection coefficient, is real and is defined as the amplitude of the reflected wave divided by the amplitude of the incident wave. As is typical of the complex form of phasors, both the magnitude and the phase of the reflection can be characterized by one compact complex constant, Γ. The complex reflection coefficient is defined as the complex reflected wave divided by the complex incident wave, both evaluated at the point of reflection (x=0 in our case). The phase shift φ is the phase of the reflected wave just after reflection minus the phase of the incident wave just before reflection (both at x=0 for our case).

We can easily check out if the above equation for the reflected wave is consistent with our description in the text. To do this evaluate the equation for the incident wave at x=0 to get:

.

The above equation for the reflected wave at x=0 gives:

.

So you see that indeed, the reflected wave equation is just the incident wave multiplied in amplitude by r and shifted in phase by φ.

Another note: there are two standard variations of the lower case phi and internet browsers are very inconsistent on which variation they use. Rest assured that         and          are the same greek letter and stand for the same mathematical quantity. The phi's occurring in equations that are entered as bit maps may be of other variation from those that have been entered as html code, depending on your browser.

The total wave field

• The total wave field consists of the sum of the two waves discussed above. Thus we sum the incident wave and the reflected wave:

  ,

  as written in the cosine notation.

• The same wave field written in the complex notation is:

  

  .     (1)

  This last equation sees extensive use in the design of electronic communication devices that use waves to transmit information.

Special cases, total reflection

• In the special case of positive total reflection, where φ=0 and r=1, then Γ=1 and the last equation becomes

  .

  This is the same as derived in the previous posting for a standing wave.

• In the case of negative total reflection, r=1 as before, but φ=180°. This makes Γ = re^iφ = -1, making our equation become:

  .

  This is similar to the above equation for the φ=0 case, however it is shifted both in position (by π/2κ) and in phase (by i = e^iπ/2 or 90°). We see this shift in the animation if we compare the standing wave pattern of the "total reflection+" case with that of the "total reflection −" case.

In the above we have used the following relationships, which are easily derivable from Euler's formula (just substitute Euler's formula in for the e^iα and e^−iα to verify these):

 (1a)

.

The standing wave ratio

The standing wave ratio is defined as the maximum amplitude in the wave field divided by the minimum amplitude:

.     (2)

This can be expressed in terms of the reflection coefficient by realizing that the maximum of the amplitude occurs where the incident and reflected waves are in phase. Look at the phasor dials in the animation above to see this (with "show components" and "total reflection" active). Similarly, the minimum occurs where the two are out of phase. When in phase they add up to an amplitude of A+rA and when out of phase they add to A−rA. Thus we can write the reflection coefficient as:

.

This equation is graphed to the right. We can also use this to solve for the reflection coefficient r in terms of the standing wave ratio s to give:

.     (3)

Position of the envelope maxima

We can also use these concepts to calculate the position at which the maximums and minimums will occur. If we are a distance  l  from the reflection, then the phase shift for the incident wave to travel up to the reflection is κl . There it undergoes a phase shift of φ upon reflection and then an additional phase shift of κl returning to our spot as the reflected wave. Thus the phase difference between the incident and reflected waves at this spot is 2κl+φ. To make a maximum, this phase difference must be an integer multiple of 2π radians. Putting this into an equation gives:

,    (4)

where n is an integer and represents the number of the particular maximum we are considering. The first maximum from the reflecting object (just to the left of the object) would have an n = 1, the second one from the object has n = 2, and so on. The wavenumber κ can be calculated from the wavelength λ (the distance between wave crests of the incident wave) as:

κ = 2π/λ.     (5)

We can solve Equation (4) for the necessary distance l for an envelope maximum to occur:

.

where φ is the phase of the reflection coefficient. Alternately, we can solve for the phase of the reflection coefficient in terms of  l:

.    (6)

The most common utility of the standing wave ratio is that it allows determination of the reflection coefficient, angle and magnitude, from simple measurements on the wave field. Observing the waves, one can obtain the wavelength λ and from that the wavenumber from the Equation (5) above. One can also measure the wave amplitudes at the maximum and minimum and calculate their ratio, or s (Equation (2) above). Using the Equation (3) above this gives the magnitude of the reflection coefficient r. Measuring the distance l from the reflecting obstacle to the first maximum and using the Equation (6) above with n=1, gives the angle of the reflection coefficient.

Location of the envelope minima

If one wishes instead to measure the distance to the minimum, then we need to alter the relationship Equation (4). In this case, we need the phase length to be some odd integer of π radians or 180° so that the incident and reflected waves will be 180° out of phase and try to cancel. So setting the phase shift due to the distance and reflection ((2κl+φ) to the odd integer of π gives:

,

where m is an odd integer (n=1, 3, 5, or 7, etc.). This can be solved to yield:

and

.

This brings us to an interesting point. The phase angle of the reflection coefficient depends critically on the location we select as the reflecting point. In some situations, this reflecting point is clear, as it was with our "total reflection+" case where there was a sheer cliff. However, often there is not an exact point that reflects the waves, such as in the "total reflection-" or "variable refl" cases. Then, in the interest of maintaining simplicity, one chooses an "effective" reflection point. With regard to the above animation, we chose the right edge of the animation, for simplicity, and calculated a set of reflection angles based on this. If we had chosen another effective reflecting point, then we would have calculated another set of reflection coefficient angles for the same total wave fields, in order to account to the different phase lengths involved with a different idealized reflection point.

Equation for the envelope

To get an equation for the envelope or magnitude of the total wave field as a function of x, we revisit Equation (1) above. One approach is to use a carefully drawn phasor diagram of Eq. (1) and the law of cosines to arrive at an expression for the magnitude of the wave field. We shall do that first. Another approach is to simply separate out the real and imaginary parts of (1), square each, take the square root, and simplify a bunch to find the magnitude. We do that secondly, below.

We do the vector sum of phasors as follows:

• To the right, we have drawn a phasor diagram (in the complex plane) showing the vector addition of the left side of Eq. (1) with the A e^iωt factored out, i.e.     
  
  
• There we see red vector representing e^iκx  is of length 1 and is drawn at an angle of κx with respect to the real axis.
  
  
• The blue vector represents  reⁱ(φ-κx)  and is of length r and angle (φ−κx).
  
  
• The angle B between the red and blue vectors is given by B = (φ−κx)−κx = φ−2κx.
  
  
• The angle C equals angle B (and therefore also equals φ−2κx ), because their two sides are parallel.
  
  
• The supplement to C, angle D, is given by D = π−C = π − (φ−2κx), where π radians equals 180°.
  
  
• By the law of cosines, the magnitude M is given by:
       .
  
  
• We can simplify the cosine:
       .
  
  
• This allows the magnitude to be written as:
       .
  
  
• Putting in the amplitude A that we left out, gives us the amplitude (half the thickness of the envelope) as a function of position:
       .

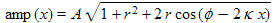  Note that A is the amplitude of the incident wave by itself.

An alternative way to derive the above expression that doesn't involve drawings of vectors is as follows:

• We start with the same complex phasor expression of incident and reflected wave, Equation (1), but we factor out half of the reflection angle as:

  .
  .
  
  

• The first factor is simply a magnitude times the complex temporal rotor times a constant phase shift. We ignore this for now and focus on the rest, which we will call M₁.   M₁ is similar to the expression for the cosine (Equation (1b) above), except for that factor of r. To get around the r, we peel off an r amount of the first term and combine it with the second term to make a cosine. Also, we still have the rest of the first term, which we put first:

  
  .
  
  

• The cosine term is totally real, so only has a real term, and the other term has both a real and an imaginary term, via Euler's formula. To take the magnitude of M₁, we use the square root of the sum of the squares of the real and the imaginary parts. So under the square root, we need to add the two real terms and square their sum, and to that add the square of the imaginary term.
  .
  
  
• We expand and combine terms and finally use the identity sin²x+cos²x=1:
  .
  .
  .
  
  
• Using the double angle formula for cosine, we get:
  .
  
  
• Symmetry of the cosine, i.e. cos(−x)=cos(x) allows us to write it as:
  .
  
  
• This is the same expression as we got above.

Practical applications of reflection concepts The concepts discussed above are of great use in modern communication systems, where electromagnetic waves carry information. These waves may be in air, in space, in a cable, or in an optical fiber. In most cases engineers seek to minimize reflection, so that the waves are almost completely absorbed by a receiver, where they are most needed and will not reflect and cause spurious ghosts or extra noise in the system. Engineers use these equations to design receivers and other components to minimize reflections and optimize other performance features. The commonly used Smith Chart is a graphical method to approach reflection problems and is based on the above equations. A biography of the inventor, Mr. Phillip Smith, is here and a very short history is here.

The animations in this posting can be downloaded free from George Mason University Archival Repository. Please read the fair use policy for this work.
© P. Ceperley, 2008.

---

NEXT: Water waves PREVIOUS TOPIC: Complex phasor representation of a standing wave

---

Good references on WAVES

Good general references on resonators, waves, and fields

Wikipedia on waves. Zona Land on waves, lots of animations. The physics classroom on waves. Thinkquest on waves. Dr. Dan Russell, Kettering University Applied Physics, nice animations. All sorts of demonstration setups and animations from the Univ. of California at Berkeley. And many more sites.... search on waves and traveling waves. Scroll down farther for a list of the various related topics covered in postings on this blog.

Think Quest -- Wave Express technorati.com The Physics Classroom HyperPhysics intutor.com Wikepedia