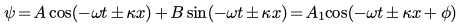| All postings by author | previous: Three types of waves: traveling waves, standing waves, and rotating waves | up: Contents of this block of postings | next: Standing waves in one dimension |
This posting includes a flash animation showing the physics discussed.
Most computers have a flash player already installed, but if yours does
not, download the free Adobe flash player here.
|
Mathematical expressions for one dimensional traveling waves
In one dimensional wave systems, traveling waves can be expressed in real form as:
or in complex form as:
| Fig. 4. Traveling wave with source and absorber. Mouse over the animation to see the action, mouse off to suspend it, and click on it to restart it. The lower object is a pipe with acoustical pressure waves propagating from the source to the absorber. The acoustical pressure is shown in color. The upper object can either be a graph of the acoustical pressure in the lower item or a depiction of waves on a string. |
where ω is the angular frequency of the wave (ω = 2π times the regular frequency, f), the + sign (of the ±) is used for waves traveling in the positive x direction and the − sign for negatively traveling waves. The wavenumber κ is related to the wavelength λ by κ = 2π/λ . κ has units of radians/meter.
A, A1, and B are real constants determining the amplitude and phase of the waves. The C has a tilda over it to indicate that it is a complex constant and sets the amplitude and phase of the complex form of a traveling wave. As is normal for the complex form, a real operator, i.e. Re( ), is understood to be required to convert the complex form into waves that exist in the real world. The complex form is used because it greatly simplifies mathematical manipulations.
The frequency and wavenumber are related by:
where c is the phase velocity of traveling waves in this particular medium at the frequency of interest. Non-dispersive waves (such as waves on a string) have a constant phase velocity while dispersive waves (such as water waves) have a phase velocity that varies with frequency. There are no restrictions on possible values of the wave number κ other than they be real (although there are applications for complex κ such as for non-propagating evanescent waves).
In the case of waves on a string, the phase velocity c, i.e. the velocity of wave propagation, is given by:
where T is the tension on the string and μ is the linear mass density of the string (kg/m).
Energy and momentum in traveling waves
From Physics of Waves chapter 1, we get the following proportionality between the energy density E1 and momentum density gx for traveling waves on a string:
gx = E1/c . (5)
There is a controversy as to whether any momentum is carried by waves on a string. This is discussed in a later posting.
| All postings by author | previous: Three types of waves: traveling waves, standing waves, and rotating waves | up: Contents of this block of postings | next: Standing waves in one dimension |