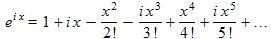Scientists who deal with oscillations and waves make extensive use complex numbers.
But just what are complex numbers and why use them?
The short answer:
Complex numbers are an invention of the handful of mathematicians in the 16th through 19th centuries. Perhaps the best known for his contribution to the development of complex numbers is Leonhard Euler. He used i, an "imaginary number" to allow him to create a relationship between two quantities that one would normally not guess to be related to each other. While "Euler's formula", (published in 1748) created interest in the mathematical community, its utility for the world at large was questionable.
By the middle and late 1800, technology associated with oscillations and waves was emerging with inventions of AC power, the telephone, and the wireless telegraph. One of the problems to be overcome was the difficulty in calculating the various design quantities associated with oscillations and waves. Engineers and scientist discovered that by using complex numbers in a rather artificial way, they were able to greatly simplify calculations.
Today, all electrical engineers and physicists are well versed in these methods and complex math is used everyday in the design of most electronics and communication devices and systems, as well as in science in general.
The long answer
A brief history of complex numbers
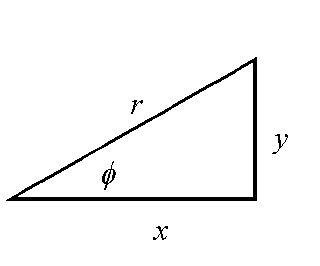
If you study trigonometry, you will be familiar with sines and cosines. Their use proved essential to navigation of the great sailing ships and today are used in countless technological computations. Their use was first documented by the Greek Hiipparchus in 140BC. They basically give you the ratio of lengths of a right triangle based on the angle involved. To be more specific, using the triangle shown below:
| 
|
the cosine is defined as
where φ is the lower case greek letter "phi". To put the above equations in words: the cosine is the ratio of the non-hypotenuse side next to the angle over the hypotenuse of that right triangle. The sine is a similar trigonometric function which uses the other side:

In text, one usually writes out "sine" and "cosine" while in an equation, we use the abbreviations "sin" and "cos" instead.
In dealing with oscillations and waves, we often consider the sine and cosine more as functions than geometric ratios. Below is an animation which shows the production of a graph of a sine function, based on the triangle above.
You will need flash on your computer to view this animation. Click on the buttons to activate the animation. Press − in the +/− button to hid the cartoon features of this animation and + to restore them.
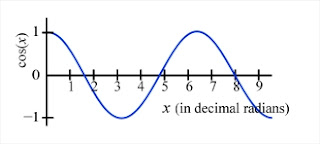
A cosine graph could be made in similar fashion, however one would need to plot x or the width of the triangle instead of its height. The graph of the cosine function is shown below plotted against angle in both degrees and radians.
In working with oscillations and waves we usually express the argument in radian. Radians are just an alternate way to measure angle. Instead of 360 degrees being all the way around a circle, in radians, it is 2 π radians or 6.28 radians is a complete circle. Because a complete circle is exactly 2 times π radians, often the angles are expressed in fractions of π as an alternate to expression the angle in decimal radians. We show both forms, both decimal radians and fractions of π above (see the numbers and labeling on the x axes.
To convert from degrees to radians multiply by π/180 or by 0.0175 . Alternately, divide by 57.30 . To convert from radians to degrees multiply by 180/π or 57.30 .
The last graph, with the red curve, is a graph of the sine function (as opposed to the cosine function) similar to that generated by the above animation, but plotted versus decimal radians instead of versus degrees. Note that the sine function is basically the same shape as the cosine function, but shifted over a little in the x axis. Actually it is shifted over exactly 90 degrees or π/2 radians.
Using calculus methods, one can show that we can use infinite series as an alternate way to express functions such as cosine and sine. The correct expressions for these are:


We have used the variable x instead of the ϕ used above (we are always free to change variables in equations, if we replace one variable with another throughout the equation). The x we use here is not the same as the x coordinate used above with the right triangle. As it is with the English language, in math, an algebraic symbol can mean different things at different times.
There is also a similar infinite series expression for e raised to a variable power x. The constant e is the base of the natural logarithms and equals 2.71828... . We show a plot of this function and its infinite series expansion below.
A relationship between sines, cosines, and ex.
In 1748 Leonhard Euler was fascinated by the similarity of these last three formulas. Indeed, at first glance it would appear that the combination of the first two formulas would contain all the exact terms of the exponential formula (the last formula). But how can that be? How can equations for trigonometry from right triangles, be at all related to exponentials that have to do with logarithms? They are usually considered totally separate and unrelated areas in mathematics. However, using the formulas we can try to relate them. It certainly looks intriguing. Plunging ahead, we find that if you simply add the first two formulas, you get:
which has the wrong signs between many of the terms, preventing it from exactly equaling ex. What is needed? These two formulas seem too close to be ignored. There must be some fundamental relationship between the trigonometric formulas and the exponential formula!
We need some way of making the signs (the pluses and minuses, not the sines and cosines) in the terms of the last formula to alternate every second term. A normal trick for adjusting signs is to insert a −x in place of the x in ex. This gives:
 .
.
Simplifying this yields:
This, however produces alternating signs every term, so it isn't quite right. Euler reasoned that he needed something with half the strength of a minus sign (or the −1) so when it was squared it would equal a minus sign. In desperation, he used a quantity i defined as:
This means that
where the ≡ stands for "defined as equal to". Euler knew this was ridiculous. Square any number (multiply it by itself) and you always get a positive number, even if the starting number is negative. So a real number with the needed properties didn't exist. Not wishing to give up so easily, he simply declared i to be "imaginary", because it only existed in his imagination, but he was going to use it anyway. Continuing, if we replace x with ix everywhere in the exponential equation, we get:
which using the definition of i can be simplified to:
We're almost there! That is, we have all the signs correct to have an exponential expression equal to the sum of the sine and cosine expression. The remaining problem is that all the terms that are associated with the sine expansion seem to have an extra i in front of them. Euler fixed that up by saying that this expression for the exponential is equal to cos x + i sin x. That is, he wrote:
This is the famous Euler's formula and is often considered to be the basis of the complex number system. In deriving this formula, Euler established a relationship between the trigonometric functions, sine and cosine, and e raised to a power. It wasn't for many years that the true power of the relationship was revealed.
Next: More details on infinite series.
Next: the technology of oscillations and waves demands new mathematical methods.
© P. Ceperley, 2007.
| Good references on WAVES | Good general references on resonators, waves, and fields |
|---|---|
|