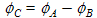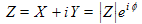More on Complex Numbers

While the phasor method does help our understanding a lot, complex math can takes it even further. It adds a convenient mathematical notation to the graphical phasor method so that we can write equations concerning wavefunction and conveniently solve for various parameters in wave related devices and phenomena. We'll next delve into complex math. I spite of the name, "complex" math, it is not all that complicated to understand, at least at the level that we use it for waves. The difficulty comes more in getting used to the strange imaginary i in our equations, in equations that deal with real objects, like bungy jumpers and communication signals.

If we multiply Euler's formula by a constant, call it A, and change the variable from x to ϕ , and set it all equal to the "complex" variable z, then we have:

,

where x = A cos ϕ and y = A sin ϕ. The number z is a general complex number with real and imaginary parts. The real part (containing no i) is x, or alternatively, Acosϕ. The imaginary part (the part multiplied by i in the formula) is y, or alternatively Asinϕ . We need to keep the terms with i in them separate because the i is an unknown quantity, something mysterious and definitely not like other numbers.

This is similar to the case in which you have an equation having many terms and some terms are simple numbers and the others have a unknown parameter p in them. For example, suppose

X = 31.4 + 4 + 23p - 11.3 - 0.9p +15.2 - 5.3p.

You can add up all the simple number terms and independently add the terms with a p in them to get

X = 39.3 + 16.8p ,

but without knowing p, you are stuck with keeping the number term and the p terms separate.

So it is with complex numbers. In general, we have a normal term, called the "real" part and also the term multiplied by the special constant i, called the "imaginary" part. When we add (or subtract) complex numbers, we add (or subtract) all the real parts together and separately all the imaginary parts together, just like we did in the above example with a p in it. Below be show some examples of this.

Starting values		Sum and Difference
A = 3.1 + 5i	B = 1 - 2i	A + B = 4.1 + 3i	A - B = 2.1 + 7i
A = −0.033 − 0.2i	B = 2 + 0.44i	A + B = 1.967 + 0.24i	A − B = −2.033 − 0.64i
A = a + b i	B = c + d i	A + B = (a + c) + (b + d) i	A − B = (a − c) + (b − d) i

Complex multiplication and division is also carried out similar to multiplying and dividing algebraic expressions containing a number term and a term multiplying an unknown p. For example, in algebra we would carry out the following multiplication as:

(2 + 3p)(1 − 2p) = (2)(1) + 3p(1) + 2(−2p) + (3p)(2p) = 2 − p + 6p² .

In complex multiplication we can proceed the same way, but at the end, we can further simply the squared term using i² = −1 :

(2 + 3i)(1 − 2i) = (2)(1) + 3i(1) + 2(−2i) + (3i)(2i) = 2 − i + 6i² = 2 − i −6 = −4 − i .

Now for division. In normal algebra, we could not simplify a division expression like:

.

In complex math, however, we can use a trick of multiplying both the numerator and denominator by the "complex conjugate" of the denominator, which will render the denominator totally real. The complex conjugate obtained by changing the sign of the imaginary term. We will demonstrate this method here:

Below are some examples of complex multiplication and division:

Starting values	Product and Quotient
A = 3.1 + 5i B = 1 - 2i	A × B = 3.1 − 1.2i − 10i2 = 13.1 − 1.2i A÷B = (3.1+11.2i-10)÷ (1+4) = (-6.9 + 11.2i)÷5 = −1.38 + 2.24i
A = −0.033 − 0.2i B = 2 + 0.44i	A × B = −0.066 − 0.4145i + 0.088 = 0.022 − 0.4145i A ÷ B = (−0.066 − 0.3855i + 0.088)÷(4+0.193) = (0.022 − 0.3855i) ÷ 4.193 = 0.00525 − 0.0782i
A = a + b i B = c + d i	A × B = (a c − b d) + (a d + b c) i A ÷ B = [(a c + b d) + (−a d + b c)i] ÷ (c2 + d2)

A graphic method for complex numbers.

To understand complex numbers more, we use a graphical plotting method which is essentially the phasor method we just discussed, however it is used for complex number use, which in general, may or may not have anything to do with oscillations. This method was first invented by Caspar Wessel in 1799, fifty years after Euler devised his formula. In this method, we plot the complex number z on the "complex plane". This is a conventional x-y graph, in which we plot the real component, x, of our complex number on the x-axis and the imaginary component, y, on the y-axis, as shown below. This is set up so that A will be the length or "magnitude" of the vector from the origin to the point we have just plotted and φ is the angle this vector makes with the x axis measured counterclockwise from the x axis. Checking, we see that the x projection of this vector is just Acosφ or x as it should be, and the y projection is just Asinφ or y as it should be.

We now have two ways to specify a complex number z. We can use the x and y, i.e. real and imaginary, components. This is called the "rectangular form" of a complex number. Or we can specify the magnitude A and "argument" φ, which is called the "polar form" of the complex number. Specifying either set of parameters will be enough to locate a point on the complex plane. We can easily convert from one representation using x = A cos φ and y = A sin φ. These can be solved for A and φ to give A = √(x²+y²) and phi; = arctan(y/x) .

Addition and subtraction on the complex plane

If we have two complex numbers, we can plot them both on the complex plane. To add these, we need to add the two x-components to form the x component of the sum and add the two y components for the y component of the sum. This is exactly like adding two 2-dimensional vectors. We can accomplish with algebraically by adding the components, just as we discussed above, OR we can add the vectors graphically with a parallelogram method discussed for vector addition, as illustrated in the diagram at the right. Subtraction can be thought of as addition with one vector first reversed in direction, just as it is in vector subtraction.

Multiplication and division on the complex plane

We will first labor through and derive equations for multiplication and division using the above results and sine and cosine identities. We will then reprove the same results using Euler's formula in an almost trivial way. First, the hard way:

From above, we see that the product of the two complex numbers

A = a + bi and B = c + di, is given by:

C = (a c − b d) + (a d + b c)i.

The magnitude or length of the vector C plotted on the complex plane is just the square root of the x component (the real part) squared plus the y component, or imaginary part, squared, i.e.:

.

Expanding the squares gives:

    ,

while canceling and combining terms gives:

    .

Finally, doing some factoring gives this result:

    .

This shows that the magnitude of the product is just the product of the magnitudes of the complex vectors A and B. Similar, albeit more lengthy, math shows that the magnitude of a complex quotient is just the quotient of the magnitudes:

,

implies

where A, B, and C are complex numbers.

---

We can now work on the polar angles. It is easier to work with the trigonometric function the tangent of the angle instead of the angle itself. The tangent of an angle is the sine of the angle divided by the cosine of the angle. If we know the tangent, we can take the inverse tangent (also called the arctangent) to know exactly what the angle is with the slight complication that we may or may not be off by exactly 180°. We'll address this again to show that it's not really a problem in this case.

The tangent of the polar angle of the complex number z = x + i t is just y/x so the tangent of the polar angle of our product is:

.

We divide both the numerator and denomator by r², we get:

.

which can be reduced to:

.

Now to address that 180° uncertainty. If we go back a couple of lines, we can repeat the same set of manipulations for both the sine and the cosine of the polar angle of the product. Knowing both the sine and cosine, does uniquely specify the angle.

This shows that the polar angle of the product vector C is just the sum of the polar angles of the two vectors multiplied together to get C, i.e.

.

Similar math shows that for the complex division C = A / B the angles just subtract:

.

Thus we see that the polar form for complex numbers results in the easiest multiplication and division rules:

• For multiplication, we multiply the magnitudes and add the angles for the new magnitude and angle.
• For division, we divide the magnitudes and subtract the angles for the new magnitude and angle.

---

Plotting e^iφ on the complex plane

We'll start off by repeating Euler's formula written with the variable φ instead of x:

.

The magnitude of e^iφ is given by:

,

and so is always equal to 1! (The identity cos²φ + sin²φ = 1 is a an altered form of the pythagorean theorem and is well known. See for example Trigonometry Solved! 2007.)

So what angle does our "unit vector" make with the x axis (the polar angle)? Suppose we try out the obvious one, φ as is drawn to the right. In this case, the real component should be 1 × cosφ = cosφ and the imaginary component should be 1 × sinφ = sinφ. Comparing with Euler's formula, just above, this is a perfect fit!

So in conclusion: in the complex plane, e^iφ is a unit vector (vector of length equal to 1) making an angle of φ with respect to the x axis as drawn above.

---

Using Euler's Formula to express a complex number in polar notation

Consider the complex quantity made by multiplying e^iφ by a real number (as opposed to a complex number):

.

The e^iφ can be used to adjust the angle to any value and the multiplier A can adjust the magnitude to any value. In short, this number Ae^iφ can take on any possible complex value. It has an advantage over the usual X + i Y notation in that it is written in terms of the polar angle (the exponent to e) and a magnitude (the multiplier A).

We can convert any complex number written in rectilinear notation Z = X + i Y to this complex polar notation by:

,

where

and

.

To convert the other way, given A and φ we use the modified Euler formula above to give the rectilinear components:

.

---

Using Euler's Formula to expedite complex multiplication and division

Suppose we want to multiply two complex numbers together. Above, we have seen how to do this in rectilinear notation. Now we do it in polar notation. Multiplying complex numbers W and Z together, we have:

    ,

where

.

We use the tilde ^~ over a variable to emphasize that it is complex. Also, we have used the fact that e^ae^b=e^(a+b). This is very important! One of the chief advantages of using complex notation is the fact that phases are handled in a elegant and efficient way. No more dealing with trigonometric identities. Instead, we just add phases as is the usual with exponents. The two rules for complex multiplication now come out naturally from the mathematical formate.

We need to point out that addition and subtraction are most easily (or ultimately) done in rectangular notation, while multiplication and division are done in polar notation.

---

NEXT: A complex representation of oscillations - complex phasors.

---

© P. Ceperley, 2007.

---

Good references on WAVES

Good general references on resonators, waves, and fields

Wikipedia on waves. Zona Land on waves, lots of animations. The physics classroom on waves. Thinkquest on waves. Dr. Dan Russell, Kettering University Applied Physics, nice animations. All sorts of demonstration setups and animations from the Univ. of California at Berkeley. And many more sites.... search on waves and traveling waves. Scroll down farther for a list of the various related topics covered in postings on this blog.

Think Quest -- Wave Express technorati.com The Physics Classroom HyperPhysics intutor.com Wikepedia