Resonances, waves and fields: How a resonator works

previous: 2.3 Strong damping - critical damping

This posting includes a flash animation showing the physics discussed. Most computers have a flash player already installed, but if yours does not, download the free Adobe flash player here.

Figure 1. Girl on a pendulum. Click on the figure to start or restart it. Mousing off and on again will stop and restart it. This animation shows the interaction of the force in the direction of motion (red vector) and the momentum (green vector). The meters and graphs indicate the force (red on graph), momentum (green on graph), potential energy (purple), kinetic energy (blue) and total energy (gray). All the scales are in "arbitrary" units. Image of animation in separate window (or tab).

Simple Resonators - Shock excitation

2.4 How a resonator works

How a pendulum works

To better understand how resonators work, let's examine one simple resonator, the pendulum, as being typical of all resonators. Examine the animation in Figure 1, the graphs in Figure 2, and the captions. The resonator uses the interplay of force and momentum in its operation. Whenever the pendulum is left or right of the center position, there is a restoring force (shown as a red arrow in Fig. 1) due to gravity, trying to push the pendulum back towards the center. When the pendulum is near the center, its momentum dominates causing it to overshoot the center and climb back up to its previous height.

We now follow the pendulum on its cycle. Suppose the pendulum is pulled to the left and released (you can freeze this condition by clicking on Fig. 1 and immediately mousing off the figure). In this position, the force is maximum in the right (i.e. positive) direction. The red force arrow is maximum and the force meter points to +1, indicating the maximum. The potential energy is also maximum here. The momentum and kinetic energy are zero because the velocity is zero.

graphs of force and momentum versus time

graphs of potential energy and kinetic energy versus time

Figure 2a. Graph of the interplay of force (in the direction of motion) and momentum in the animation of Figure 1. Because force and momentum have different units, the vertical scales of the two curves are different. The force peaks precede the momentum peaks. The interplay of the two quantities are set by Newton's second law, F = dp/dt where F is the force, p is the momentum, and t is time. Momentum is defined as p = mv, where m is the mass, v is the velocity. Verbally, Newton's second law says that an unbalanced force on an object will cause a change in the momentum of the object where the time rate of change of the momentum will equal the force.

Figure 2b. Graph of potential energy, kinetic energy, and total energy versus time for the animation of Figure 1. There a several differences between this graph and Fig. 2a. These differences are mostly due to the potential and kinetic energy being proportional to the square of sinusoids instead of proportional to the sinusoids themselves as in Fig. 2a. First the frequency of oscillation is doubled. Secondly, these quantities are always positive. The potential energy (PE) is maximum when the pendulum is at the extreme left or right, i.e. when the bob has the maximum height, PE = mgh where g is the acceleration of gravity, and h is the height above some fixed reference height. The kinetic energy (KE) is maximum when the bob has its maximum velocity which occurs when the bob is at its lowest point, KE = (½)mv².

The pendulum responds to the right pointing force and begins to swing towards the right (created in the animation by mousing back on the figure or clicking "step" once or twice). As the pendulum swings down, its speed, momentum, and kinetic energy build up. At the same time, the force and potential energy, which are proportional to the distance from center, decrease. We say that potential energy is being converted into kinetic energy.

When the pendulum reaches the center, the force on it and the potential energy are zero. The velocity, momentum, and kinetic energy are maximum, having been built up by the earlier application of force (governed by the equation p = ∫Fdt which is an integration of Newton's second Law).

If the force were all that mattered, the pendulum would stop in the center where the force is zero, but there's also momentum to consider. When the pendulum reaches the center, the momentum is a maximum, and it is this momentum that carries the pendulum past the center. It fact on the right side of the center, the force is actually negative, fighting the momentum as the pendulum swings, slowing it down. However, the momentum is substantial and carries the pendulum up to its right-most position. If the pendulum has low loss, the bob will swing up to the same height it started with, on the opposite side. During this swing up on the opposite side, while the pendulum is slowing down, the process now converts the kinetic energy back into potential energy.

This interplay of force and momentum occurs again and again, as graphed in Figure 2a. Note that the green momentum graph peaks after the red force graph does. That is to say, that after a interval of time with positive force, the momentum becomes positive. After an interval of time with negative force, the momentum becomes negative.

Figure 2b graphs the interplay of potential and kinetic energy. These energies are always positive. (Technically, the potential energy can contain an additive or subtractive constant that could make it negative, but most people choose the constant to make the potential energy zero at the lowest point on the pendulum swing.) When the potential energy is maximum, the kinetic energy is zero. When the kinetic energy is maximum, the potential energy is zero. The sum of these two energies equals the total energy, which does not cycle. In the case of a lossless pendulum, the total energy stays constant, as shown with a dashed line in Figure 2b. A real pendulum will have a slight amount of loss, which will cause the total energy to decrease in time in an exponential decay. We will discuss that more in the next posting.

Table 1. Restoring force on a pendulum.
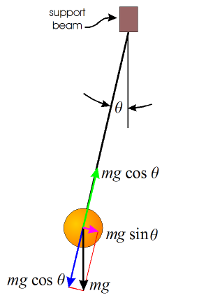
At right is a diagram of a pendulum showing the forces on the bob (which has a mass, m). Gravity exerts a force of mg in the downward direction (shown in black). The string exerts a counter force of mg cosθ upward^* along the direction of the string (shown in green). The black gravity force can be separated into the purple and blue forces. The blue force counters the green string tension force. There is a net unbalanced force of mg sinθ (shown in purple) along the direction of motion of the bob. ^The string tension deviates slight from mg cosθ to make the bob move along a curved path. We can ignore this for the current discussion.* The purple force is the "restoring force" which is responsible for motion of the bob. If angle θ is much less than one radian, then we can approximate sinθ with θ, the restoring force is proportional to the displacement angle θ, and the pendulum is isochronic meaning that its period is independent of the size of its swings. Thus a swing of θ = 3° will have nearly the same period as a 6° swing has, while a 30° (which approximately equals half a radian) swing will have a substantially different period. For small angles the restoring force is equal to mgθ . This means that Newton's second law becomes: (1) which simplifies to , (2) where v = r dθ/dt is the bob velocity during the swing, and r is the pendulum length (from the pivot point to the center of the bob). This is the standard second order differential equation listed in Section 1.0. It has a solution: , (3) which is basically the same equation as we discussed for the LRC circuit resonator in Section 2.1, Equation (1) and Section 2.2, Equation (6b) .

Table 1. Restoring force on a pendulum.

At right is a diagram of a pendulum showing the forces on the bob (which has a mass, m). Gravity exerts a force of mg in the downward direction (shown in black). The string exerts a counter force of mg cosθ upward^* along the direction of the string (shown in green). The black gravity force can be separated into the purple and blue forces. The blue force counters the green string tension force. There is a net unbalanced force of mg sinθ (shown in purple) along the direction of motion of the bob.

^*The string tension deviates slight from mg cosθ to make the bob move along a curved path. We can ignore this for the current discussion.

The purple force is the "restoring force" which is responsible for motion of the bob. If angle θ is much less than one radian, then we can approximate sinθ with θ, the restoring force is proportional to the displacement angle θ, and the pendulum is isochronic meaning that its period is independent of the size of its swings. Thus a swing of θ = 3° will have nearly the same period as a 6° swing has, while a 30° (which approximately equals half a radian) swing will have a substantially different period.

For small angles the restoring force is equal to mgθ . This means that Newton's second law becomes:

(1)

which simplifies to , (2)

where v = r dθ/dt is the bob velocity during the swing, and r is the pendulum length (from the pivot point to the center of the bob). This is the standard second order differential equation listed in Section 1.0. It has a solution:

, (3)

which is basically the same equation as we discussed for the LRC circuit resonator in Section 2.1, Equation (1) and Section 2.2, Equation (6b) .

A general resonator

All mechanical resonators (see Fig. 1, section 1.0 for examples) work on the same principles as the pendulum above. They all use the interplay of a restoring force and momentum of a mass. The restoring force continually pulls the resonator back to its equilibrium configuration, while the momentum causes it to overshoot the equilibrium configuration, again and again in a cyclic manner. In all these resonators, graphs of force, momentum, and energies would look just like those in Figures 2a and 2b above.

The LRC circuit is an electromagnetic resonator. In this resonator, the charge on the upper capacitor plate is analogous to the displacement in a mechanical resonator. The capacitor provides a restoring voltage (analogous to the restoring force) and tries to force the charge to be zero. The inductance provides a "momentum" to the current flow, mathematically the same as the momentum in a mechanical resonator. The inductance prevents rapid changes in the flow of charge, i.e. in the electrical current. This causes the charge to overshoot and cycle around the zero value in a sinusoidal fashion, similar to the action in a mechanical resonator. Instead of the force and momentum interacting, in the LRC circuit, the capacitance voltage and the quantity LI interact where L is the inductance and I is the electrical current passing through all three circuit elements (the inductor, resistor, and capacitor). The "resistor" may be an actual separate circuit element (as seen in Fig. 3 of an earlier posting) or just the inescapable resistance of all inductors and capacitors. In place of the potential and kinetic energies of Fig. 2b above, the LRC resonator involves the cycling of electric and magnetic energies in the capacitor and inductor, respectively. The electric energy (a potential energy) is proportional to the capacitance charge squared ( U_C = (½)q²/C ), while the magnetic energy (a kinetic energy) is proportional to the current squared ( U_L = (½)LI² ).

There are many other types of electromagnetic resonators, a few a which we will discuss in future postings.

In general, there are many, many types of resonators. Those that are linear, behave in a very similar fashion to the pendulum discussed above. An earlier posting showed a handful of these. It also listed the variables that were analogous to the displacement and momentum of the pendulum. In a future posting, we will explain resonators that have multiple modes of oscillation. Each of these modes can be mathematically modeled as the pendulum above or as the LRC circuit.

As to the mathematical analysis of the pendulum's motion or the behavior of any other linear resonator, we can draw on the math we used for the LRC circuit in an earlier posting.

P. Ceperley March 2010