| All postings by author | NEXT: 2. Shock excitation |
1. Simple Resonators - Introduction
A resonator is a structure that can be excited into oscillations at a specific frequency.
There are many types of resonators. They are the essential part of our musical instruments, our voices, our clocks, and many electronic and communication circuits. They are found throughout natural phenomena: from tiny microscopic atoms, atomic nuclei, atomic transitions, to huge astronomical resonating suns and stars. Major types of resonators include acoustical resonators such as organ pipes and flutes, mechanical resonators such as bells, tuning forks and quartz crystals, electronic resonators such as LRC circuits, and atomic resonators which involve the electrons in atoms. Resonators can be linear and non-linear; however, for the most part we will restrict this discussion to general linear resonators, whose properties are independent of excitation level and set instead by the dimensions and construction of the resonator itself.
We start by considering simple resonators, such as those shown below in Figure 1. Mouse over the resonator images to see them in motion. Click on them if they don't start. Half of them (the third through the fifth) are animated in slow motion, much much slower than in real life.
| Fig. 1. Examples of simple resonators | Defining equations | |
|---|---|---|
| Pendulum. This simple resonator was the heart of the pendulum clock. Such clocks were the best time keepers up through the first part of the 20th century. Long ago, Galileo discovered that a pendulum's period is a function only of its length. Read about the history of pendulum clocks here. | The governing homogeneous (without external stimuli) differential equation is
written in terms of the displacement angle θ and pendulum length r. It is valid for small amplitudes of swing, θ<<1. R is the resistance to motion, usually from air friction or coupling to a non-rigid support. The resonant angular frequency is
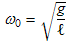where g is the acceleration of gravity and
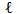is the pendulum length (measured from the pivot point to the center of the mass). Surprisingly, the frequency is independent of the mass of the bob, however it does depend on the swing amplitude for large amplitude swings.
| |
| Mass and spring. This resonator is used by many physicists as the elemental simple mechanical resonator, to explain the properties of more complex resonances and resonators. It has the advantage over electrical resonators (such as the LRC circuit below) in that one can directly observe the oscillations, making it great for classroom demonstrations. Perhaps the closest common object that resembles this resonator is the bobble head doll. | The governing homogeneous differential equation is
written in terms of the vertical displacement y from its equilibrium position, mass m and spring constant
 .
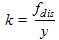The angular resonant frequency is given by
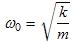where k is the spring constant. Surprisingly, the force of gravity does not appear in the equations when they are written in terms of the vertical distance y from the equilibrium point.
| |
| LRC circuit. Electrical engineers and elemental physics textbooks commonly use this as the elemental resonator. It requires an oscilloscope and signal generator to observe the resonance. It has applications in much of modern electronic technology. | The governing homogeneous differential equation is
written in terms of the charge q on the top plate of the capacitor. The resonant angular frequency is given by
where L is the inductance, R is the resistance, and C is the capacitance. The red arrows in the animation show the flow of charge, i.e. the electrical current, during the cycle. The green arrows represent the magnetic field and the red shading represents the electric field, both of which store energy.
| |
| Acoustical Helmholtz resonator. This is the acoustical equivalent to the LRC circuit. It consists of a closed space with a small passageway to the outside, such as a wine bottle, that functions as an acoustical resonator. It is named after Hermann von Helmholtz (1821-1894) who promoted this resonator. | The governing homogeneous differential equation is
 ,
written in terms of y, the vertical displacement of gas in the neck from its equilibrium position; ρ, the gas density; S, the cross-sectional area of the neck; L, the length of the neck;
 ,
a neck length correction factor;
γ
is the ratio of specific heats of the gas, and a is the neck radius. The angular resonant frequency is
where
is the velocity of sound.
| |
| Tuning fork. These are commonly used to tune pianos. Miniature versions of these are used in modern "quartz" watches and clocks to keep time. | The governing homogeneous differential equation is
written in terms of the tip displacement x from equilibrium. The angular resonant frequency is
where k is the spring constant of the tips for lateral deflection, meff is the effective mass of the tips,
α
equals 3.52 for the fundamental mode, a is the width of one of the vibrating fingers,
is its length, E is the modulus of elasticity of the material, and ρ is the density of the material.
|
|
| Balance wheel. These were used for many years as the timing element of pocket watches and clocks. | The governing homogeneous differential equation is
written in terms of the displacement angle θ of the balance wheel from its equilibrium angle, an angular spring constant
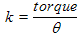due to the spring (torque per deflection angle), and I is the moment of inertia of the balance wheel. The angular resonant frequency is
in terms of the same constants.
| |
While each resonator has unique properties, it also has properties that are common to all resonators. This can be considered as stemming from the fact that they are all governed by a simple linear second order differential equation. As we see in Figure 1, all have governing equations of the form
where the constants A, B, and C are different for the various resonators. For example, we can see that the inductance L in the LRC circuit plays the same role as the mass m of the pendulum bob, both being the coefficient A (of the second order term).
The different resonators also have different variables, which we will call the "oscillating parameters". Fig. 2 lists equivalent oscillating parameters for these six resonators. In Figure 2, we list three types of these parameters: displacement, kinetic and potential parameters. Looking at Figure 2 we also notice that for any particular resonator, these three types are related by simple linear equations. Because all three types of variables are linearly related, they respond similarly to external stimului. Because of the similarity, people are inclined to use any of the variables as good indicators of the resonance. Thus, while the differential equation for an LRC circuit resonator may be written in terms of the charge q(t), the standard experiment to observe its resonance involves observing, not the charge, but the voltage across the capacitor, because it is much easier to monitor the voltage, and the voltage is proportional to the charge.
The kinetic and potential parameters are especially useful in describing the kinetic and potential energies in a resonator. We also need to note that while these parameters are related to energy, none of them are energy or power themselves. Instead, because the energy and the power are proportional to the square of the appropriate parameter, we need to keep energy and power in a different mental category than the oscillating parameters listed in Fig. 2.
| Figure 2. Equivalent oscillating parameters in simple resonators | |||
|---|---|---|---|
| resonator type | displacement parameter | kinetic parameter | potential parameter |
| Pendulum | Angular displacement of bob, θ |
Velocity of bob,
|
Restoring force on bob (due to gravity),
|
| Mass and spring | Vertical displacement from equilibrium of mass, y |
Vertical velocity of mass,
| Restoring force of spring, fres = ky |
| Series LRC circuit | Charge on top plate of capacitor, q |
Current through all circuit elements,
| Voltage across the capacitor, VC = q/C |
| Helmholtz resonator | Vertical displacement from equilibrium of gas in neck, y |
Vertical velocity of gas in neck,
|
Restoring force on gas in neck,
|
| Tuning fork | Horizontal displacement of one finger tip, x |
Horizontal velocity of that finger tip,
| Restoring force on finger tip from the metal below it, fres = kx |
| Balance wheel | Angular displacement of wheel, θ |
Angular velocity of balance wheel,
| Restoring torque of spring, torque = kθ |
Note that the oscillating parameters of Fig. 2 are often variously referred to as "signals", "wavefunctions", "oscillations" or "waves" depending on the situation and the whim of the writer.
Figure 1 above also gives the angular resonant frequency of each of these resonators. The resonant frequencies and other properties common to all simple resonators will be discussed in the next chapters. We will use an LRC circuit as a model for all resonators. Indeed, many simple mechanical resonators such as those in Figure 1 are directly analogous to LRC circuits as we have just seen. On the other hand, most of the resonators have many modes and require field solutions to accurately predict these modes and fields. However, even in these systems we can use a lumped parameter model for each mode [Ramo, pp 515-8], the LRC circuit perhaps being the most widely used of these models. It is for this reason that we explore various aspects of LRC resonators as a typical example of all simple resonators and modes of resonators. To derive the various resonator equations we will use the LRC circuit model in terms specific to that resonator, but where possible, will then convert the equations into universal terms that are directly applicable to all resonators.
| P. Ceperley, Jan. 2010. |
| ||
|
