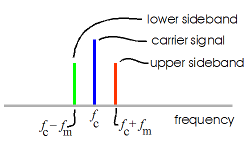Resonances, waves and fields: up/down conversion, an application of phasor multiplication

previous: 2.9 Modulation, application of phasor multiplication

2.9a Up/down conversion, an application of phasor multiplication
Keywords: up conversion, down conversion, power transfer, phasor multiplication.

Another widely used application of phasor multiplication and mixers is up and down conversion (or heterodyning) of communication signals. Virtually every radio and television in use today uses down conversion, and virtually every broadcast system uses up conversion. Today's televisions, and AM and FM radios commonly receive a signal at whatever frequency the television station or cable company is broadcasting, use a mixer to change the frequency of the signal to a fixed IF or intermediate frequency, (often 10.8MHz) and then run the intermediate frequency signal through a set of filter-amplifier stages before demodulating the signal and sending it to other electronic stages. The filter-amplify stages at the fixed frequency are able to very effectively separate the signal from other signals (such as from adjacent broadcast stations), as well as amplify the signal very efficiently to a preset level so that it is useful for producing the intended sound (in the case of radios) or images and sound (in the case of televisons).

Up conversion is basically the same process as AM modulation covered in the previous posting; however conceptually, it is more generalized. Instead of thinking of it as something you do to a carrier signal (i.e. as a modulation of that signal), up and down conversion is thought of as a change of frequency of a signal, e.g. a voice signal from a microphone is "up converted" to the carrier frequency.

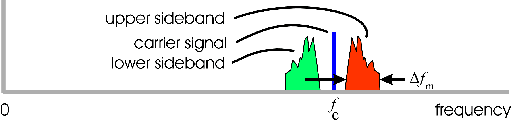
The essence of the up conversion process can be seen in Table 3 of the preceding posting that dealt with modulation. The relevant images are reproduced in Fig. 1 below. Looking at Fig. 1a, we see that the signal from the microphone is mixed (multiplicatively, not additively) to the signal of a local oscillator. In Fig. 1b we see the "Fourier series strengths" which shows the original signal having changed from frequency f_m to two frequencies: f_c − f_m and f_c + f_m . These new frequencies are called the "difference" and "sum" frequencies. In a typical up or down conversion process, a filter is used to select one of these frequencies for further use. The filter would also remove the "carrier signal" shown in the graph, if desired. Fig. 1c shows the spectum that results from the mixing process if the original signal f_m is not a single frequency, but has a range of frequencies, as would normally be the case for communication signals.


Fig. 1a. Image from previous posting showing AM modulation of a constant oscillator signal using the time varying signal from a microphone.	Fig. 1b. Image from a previous posting, showing the frequency spectrum resulting from the AM modulation of a constant oscillator signal by a lower frequency signal of frequency f_m.


Fig. 1c. Image from previous posting showing possible spectrum of signal from microphone.	Fig. 1d. Image from previous posting showing spectrum resulting from the spectrum of Fig. 1c modulating a constant "carrier" signal of frequency f_c.

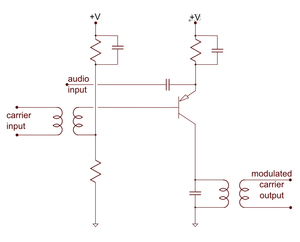
As we saw in the preceding posting, a (multiplicative) mixer typically receives two frequencies (typically a received "RF" signal and a "local oscillator" or "LO" frequency) and from these produces both sum and difference frequencies on the output. Central to a mixer is a non-linear element that creates these frequencies. A commonly used component for the non-linear element is a set of diodes which do the mixing as shown in Fig. 2b. Also comonly used is a transitor or FET as shown in the circuit in Fig. 2c. In the next section we explore the mathematics of mixing as done with a passive non-linear element, a non-linear capacitor which could in principle be lossless. Examining a passive non-linear element allows us to examine the mixing process without the complication of losses (or gains) as are present with diodes, transistors and FETs. In practice, passive elements are usually used only at optical frequencies for up and down conversion of signals carried by optical fibers.

Figure 3 below shows a block diagram of an up/down converter circuit using the mixer and the spectra of the signals at various points in the circuit.


Fig. 2a. Typical commercial multiplicative mixer. This style is typically used at microwave frequencies (100MHz and above). The internal circuitry is sketched in Fig. 2b.	Fig. 2b. Internal circuitry of a multiplicative mixer using diodes as the non-linear (i.e. multiplicative) element. This circuit is typical of "double balanced" mixers. The double balance type mixers attempt to pass only the product signals through and none of the original signals. There are many companies that sell these devices (search under "microwave mixers").	Fig. 2c. Typical mixing circuit using a PNP transistor as the non-linear (i.e. multiplicative) element.

Fig. 3a. Block diagram of an up/down converter circuit. If one looks carefully at the circuit shown in Fig. 2c, one sees a filter (a capacitor and inductor in parallel) on the output of that circuit, meaning that the circuit of fig. 2c has all the elements of an up converter circuit.


	↑ Fig. 3b. Spectra of signals at various points in the circuit shown in fig. 3a, assuming it functions as an up converter. The first spectrum is that of the two pure signals entering the mixer (a composite of the two inputs of the mixer shown on one graph.) The second shows the output of the mixer having remnants of the local oscillator signal and the two sidebands, i.e. the sum and difference signals. The third spectrum is the output of the filter, showing only the desired upconverted signal remaining.

Mathematics of frequency conversion

Three frequencies

There are three frequencies of interest here:

f₁ and ω₁ are the frequency and angular frequency of the first signal, i.e. of the input signal to be up converted.
f₂ and ω₂ are the frequency and angular frequency of the output filter (a resonator acting as a filter), i.e. the output signal after up conversion. This filter selects the "sum" frequency.
f_m and ω_m are the frequency and angular frequency of the local oscillator. The oscillator frequency is chosen to equal the difference between the above two frequencies, i.e.

f_m = f₂ − f₁ and ω_m = ω₂ − ω₁ . (1)

In contrast to the previous posting, here we label the local oscillator frequency as f_m and view it as being the modulator of the input signal. Because f₁ and f_m are to be multiplied, we could choose to view either signal as the "modulating signal" and the other signal as the "modulated signal". Mathematically they are both treated the same.

A non-linear capacitor

We consider the case where we apply all three of these frequencies simultaneously to a non-linear capacitor, a capacitor whose capacitance varies with the voltage V applied across the capacitor:

C = C₀ + αV , (1a)

where α is a constant. For the purposes of this derivation, we will ignore the constant part of the capacitance, which does not participate in the mixing, and let the capacitance instead be given by

C = αV , (1b)

i.e. the case where the capacitance is proportional to the applied voltage.

The signals, real and complex notations

The signals at these three frequencies in real notation are given by:

V₁ = v₁cos(ω₁t + φ₁) , V_m = v_mcos(ω_mt + φ_m) , and V₂ = v₂cos(ω₂t + φ₂) , (2)

where the total voltage on the capacitor is the sum of these:

V_total = V₁ + V_m + V₂ = v₁cos(ω₁t + φ₁) + v_mcos(ω_mt + φ_m) + v₂cos(ω₂t + φ₂) . (3)

The complex notations for these voltages are:

(4) and

, (5)

where the tildes, ~, over various quantities are to remind us that these are complex. Note that the magnitudes contain a complex phase shift which can be broken out as:

complex forms of amplitudes of the signals

, (5a)

where the amplitudes without tildes are assumed to be the amplitudes of these which are simple real numbers.

Another thing to remember is that complex notation assumes that the actual signals are the real part of the complex notations as written. This "real part of" or Re( ) is seldom written, but assumed to always be there. The complex notation is used for computational efficiency, i.e. for most calculations it greatly simplifies the algebra involved. For more on this see my earlier posting.

Current through the non-linear capacitor

The current through a capacitor equals the capacitance times the time rate of change of the voltage across it, which means for our capacitor defined by (1b) we have:

, (6)

where C = dQ/dV is the differential (i.e. small signal) capacitance given by (1b) above. We see from (6) that in the case of an extreme non-linear capacitor given by (1b) above, the equation for the total current contains a product of two oscillating quantities (V and the derivative of V) . In a previous posting, we discussed the problem with taking such a product in the complex notation. We could avoid complex notation and simply use the real notation for the rest of this derivation, however this makes for a very lengthly derivation. Instead we will use a complex method discussed in that same posting that involves using the real part of one of the two phasors:

, (7)

where Re() means "real part of" and the asterisk * stands for the complex conjugate. The real part of any complex quantity can be had by taking one half of the quantity added to its complex conjugate (as is done in (7) ).

Before we go further we will take the time derivative of (5) as called for in (7):

. (8)

Multiple frequencies

In this section we shall expand (7), which will produce a variety of new frequencies: double frequencies, difference frequencies, and sum frequencies. We shall discard any of these new frequencies that do not interest us and only keep the three frequencies ω₁, ω_m, and ω₂. We assume that these three frequencies are either driven input frequencies or frequencies that have resonances (i.e. filters) associated with them (as illustrated in Fig. 3) that make them very sensitive to these signals, while the other mixed frequencies do not and produce no important effects.

Substituting (5) and (8) into (7), we get:

. (9)

Multiplying the parts of the two main terms together while saving only our special three frequencies, we have:

. (10)

Using (1), this can be simplified as:

. (11)

We next make use of the fact that there is an implied "real part of" in the complex notation we are using and also that the "real part of" a complex quantity equals the real part of its complex conjugate. Thus:

. (12)

Applying (12) to (11), we have:

. (13)

Using (1) again, this becomes:

. (13a)

We see that the current at each frequency through this extremely non-linear capacitor is proportional to that frequency and to the amplitudes of the two other frequencies that have mixed together to produce this frequency. We have further emphasized each frequency component by labeling each in a special labeled pair of parentheses.

Average power flow

The formula for finding the power flow averaged over the various oscillating cycles using complex notation is P_ave = ½Re(I⋅V^*) . Substituting (5) and (13) into this, we have:

, (14)

where the real part operator is taken over both the last 70% of the first line and the entire second line.

We next simplify (14) saving only non-oscillating terms (we are interested only in the average power flow):

. (15)

Next, we use the second relation in (12) on the last term of (15) and then factor out the product ω^*₁v^*_mv₂ .

. (16)

Further simplying we have:

, (17)

where −ω₁ is the proportionality factor for the power delivered at frequency ω₁, −ω_m is the proportionality factor for the power delivered at frequency ω_m, and ω₂ is the proportionality factor for the power delivered at frequency ω₂. That is to say, except for the signs, the signal at each frequency delivers or absorbs power in proportion to the magnitude of its frequency.

Also, because ω₁+ ω_m= ω₂ (equation (1) above) the total power flow into or out of the capacitor is zero, as it should be for a passive element. We also see that ω₁ and ω_m are linked, in that they both have the same sign of power flow: the power either flows out of ω₁ and ω_m and into ω₂, or it flows from ω₂ and into ω₁ and ω_m.

We can further simplify (17) by using the relations shown in (5a) expressing the complex amplitudes in terms of a magnitude and phase:

, (18)

where we have dropped labeling each power flow to simplify the result.

In (18) we see that the power flow into or out of a particular frequency is equal to the product of:

one fourth,
the non-linear constant α of the capacitor,
the magnitudes of the three frequencies,
the particular frequency (ω₁, ω_m, or ω₂), and
the sine of the phase difference φ₁ + φ_m − φ₂ .

Other applications of the above math

The above result would also apply exactly for a non-linear inductor, except for the replacement of the non-linear constant in the capacitance with that for the inductor: L = L₀ + αI . Note also that the roles of current I and voltage V are interchanged when going from the capacitor case to the inductor case. The math for a mixing circuit employing a non-linear resistor would be derived in a very similar fashion as the above, with the expectation that there would be an additional power loss due to the resistance.

We should reiterate that the above derivation assumes that the circuitry associated with the non-linear capacitor blocks many of the frequencies (such as the double frequencies) so that no appreciable power flow would be be allowed at these unwanted frequencies.

Fig. 4. To cause an atomic electron to change its energy level from E₁ to E₂ (where E₂ > E₁) a photon must have a frequency of f = (E₂−E₁)/h , where h is Planck's constant, a fundamental constant of quantum mechanics. The above up/down conversion math, when applied to an atomic transition, predicts that the energy transfered at each of the three frequencies involved will be proportional to that frequency.

Application to quantum mechanics

The above derivation may also be applied to energy level transitions in an atom as discussed in quantum mechanics. We can view f₁ and f₂ as the frequencies of two energy levels of an electron in the atom, and f_m as the frequency of an external electromagnetic wave (or photon) impinging on the atom. Each energy level represents a resonance, i.e. a filter of sorts with a potential signal at its resonant frequency. The electron's coupling to external electromagnetic waves represents a non-linear mixing term in the Hamiltonian of the electron that allows coupling between the two resonances (i.e. energy levels), in much the same manner as the two electronic signals at frequencies f₁ and f₂ in the math above are coupled by the non-linear capacitor and the modulating signal at frequency f_m.

If we assume that the energy level E₁ corresponding to f₁ is initially excited (i.e. the electron is in that energy state), and the two energy levels and the external wave all couple passively through the charge of the electron, then based on the above math we would expect the energy should flow from the first energy level (f₁) and the external electromagnetic wave (f_m) in amounts which are proportional to the frequencies f₁ and f_m. The amount of energy deposited in energy level E₂ will likewise be proportional to its frequency f₂. While the classical arguments presented here do not address the idea of quantization of the energy in packets of hf and the proportionality constant h, these classical arguments do predict that the amounts of energy transfered at each frequency will be proportional to that frequency consistent with quantum mechanics. In a future posting we hope to do the math using the Hamiltonian and quantum mechanical variables of an electron in an atom in the presence of an electromagnetic wave. The math with strongly parallel the work above.