There are all sorts of resonances around us, in the world, in our culture, and in our technology. A tidal resonance causes the 55 foot tides in the Bay of Fundy. Mechanical and acoustical resonances and their control are at the center of practically every musical instrument that ever existed. Even our voices and speech are based on controlling the resonances in our throat and mouth. Technology is also a heavy user of resonance. All clocks, radios, televisions, and gps navigating systems use electronic resonators at their very core. Doctors use magnetic resonance imaging or MRI to sense the resonances in atomic nuclei to map the insides of their patients. In spite of the great diversity of resonators, they all share many common properties. In this blog, we will delve into their various aspects. It is hoped that this will serve both the students and professionals who would like to understand more about resonators. I hope all will enjoy the animations.

For a list of all topics discussed, scroll down to the very bottom of the blog, or click here.

Origins of Newton's laws of motion

Non-mathematical introduction to relativity

Three types of waves: traveling waves, standing waves and rotating waves new

History of mechanical clocks with animations
Understanding a mechanical clock with animations
includes pendulum, balance wheel, and quartz clocks

Water waves, Fourier analysis


Thursday, March 31, 2011

Power loss in resonators

All postings by author previous: 2.5 Energy in a resonator up: Simple resonators - Contents next: 2.7 Energy and power by complex methods

2.6 Power loss in resonators

In the previous posting we derived approximate equations for the power loss and energy in a resonator as a function of time. The approximate formulas were:

         P = αU   ,   (a)    and     U = U0 e−αt     ,   (b)

We can combine these to get      P = αU0 e−αt = P0 e−t/τenergy   ,   (c)

where P0  = αU0 is the initial power loss (at t = 0 ) and τenergy = 1/α is the time constant for the decay of energy and power.


Rate of energy loss in a shock excited LRC circuit resonator

Next we calculate the power loss in an LRC circuit resonator using the formulas we derived in the last posting. This should give us a more precise formula for the power loss than Equation (c) above.

Table 1. Derivation of -dU/dt in a shock excited LRC resonator.
equation of energy in a shock excited LRC resonator (1a) This is a copy of the equation we derived for the energy in a shock excited LRC resonator in the Equation (1j) in the last section.
minus first derivate of U (1b) We start the process of taking the first derivate of Equation (1a)  (of U(t) ) with a minus sign .
minus first derivate of U - results (1c) We have combined similar terms.

Equation (1c) is graphed below in Figure 1c. We see that the power is a pulsating decaying waveform. The frequency of pulsing is twice that of the charge oscillations of Figure 1a (you can see that both in the figure and in Equation (1c) where there is a new "2" in the arguments of the sine and cosine terms compared with Equation (1d) of the previous section for the charge oscillations.) Except for the pulsating nature, the decay of power is very similar to the decay of energy. That is, it is an exponential decay with a time constant equal to that of the energy decay (Figure 1b). The power decay time constant is equal to half of the time constant for the decay of the oscillating charge of Figure 1a.

We also see the average power loss in Figure 1c, graphed versus time. This average power is given by first factor in Equation (1c), i.e. as

    Paverage = A2/Cτ exp(−2t/τ)  .

This represents a moving-averaged power, averaged over one period of the pulsating power. These average results are consistent with Equation (c) above, where τenergy = τ/2.

If we had a resonator in which the power loss was proportional to the potential energy, instead of the kinetic energy, we would see a similar pulsating nature, except that the pulses would be shifted in time, to occur at the peaks of the potential energy instead of the kinetic energy. It is more common for losses to be associated with kinetic energy, however some resonators do have losses proportional to potential energy or some mix of the two (or even to some other factor such as due to sliding friction).

decaying oscillation of LRC circuit decaying energy in LRC resonator decaying power loss in LRC resonator
Figure 1a. Decay of oscillating charge in an LRC circuit resonator. Figure 1b. Decay of energy versus time in an LRC circuit resonator. Figure 1c. Pulsating power loss versus time for an LRC circuit resonator.

Power loss in the resistor of an LRC circuit resonator.

The power loss in an LRC circuit is entirely in the resistor. That loss is given by Presistor = I2R . Next we calculate this to check that it indeed equals the result we obtained above, i.e. Equation (1c).

Table 2. Derivation of power loss in a shock excited LRC resonator.
electrical current in a shock excited LRC resonator (2a) We repeat an earlier equation for the current in a shock excited LRC circuit resonator as a starting point.
power dissipated by the resistor (2b) This is a standard equation for the power dissipated by a resistor. We substitute the current from Equation (2a).
simplification of (2b) (2c) We have used sin2θ = 1 − cos2θ and also 2sinθcosθ = sin(2θ) .
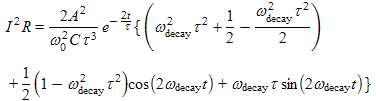further simplification (2d) Here we used cos2θ = ½+½ cos2θ .
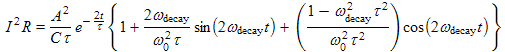power dissipated by the resistor - results (2e) This is our final result. We used the relation ωdecay2 = ω02 − 1/τ2 to reduce the constant term inside the braces of Equation (2d) to ½. We see that Equation (2e) is indeed equal to Equation (1c), showing that −dU/dt = Presistor .


Comparing the results in Equations (1c) and (2e) we see that −dU/dt = Ploss at least in the case of the LRC circuit resonator. It also points out that there are two ways to calculate the power loss. It is often true with physical parameters that there are several ways to calculate a particular quantity, which is good because often one method is easier to use or easier to understand.

P. Ceperley Feb. 2010
All postings by author previous: 2.5 Energy in a resonator up: Simple resonators - Contents next: 2.7 Energy and power by complex methods

Posted by P. Ceperley at 4:31 PM