Resonances, waves and fields: 2.8 A valid method of multiplying two complex phasors

previous: 2.7 Energy and power in a resonator by complex methods

2.8 A Valid method of multiplying two complex phasors

Summary

If two complex phasors are simply multiplied together, the result is not valid and differs from what is obtained by multiplying two real sinusoidal waveforms.
The standard work around, i.e. ½ψ₁ψ₂, averages out the high frequency components and is consequently valid only for the low frequency components.
The method discussed in this posting involves multiplying one complex phasor by the real part of the second complex phasor:
product = ψ₁Re(ψ₂) = ½ψ₁(ψ₂ + ψ₂)

where ψ₂ is the complex conjugate of ψ₂
This method produces a product that agrees with the more laborious result obtained by multiplying two real sinusoidal function together and is therefore valid.
This method preserves all frequency components of the product.
Details, further explanations, and examples are contained in this posting.

In previous postings we have stated that there are no standard methods for multiplying two complex phasors together. The problem with multiplying two phasors was explained in detail in the last posting. We also gave the standard work-around which gives the product averaged over the phasor cycle. In this section we present an alternate complex method that seems to give valid results and does not average out the higher frequency dependence. While this method was independently stumbled upon by the author, it is a big world and is most certainly previously known by others.

The problem with multiplying two complex phasors together

The general problem is as follows. Signals and other phenomena can be mathematically represented by sinusoids of the form:

y(t) = A cos(ωt + φ) , (1)

where A is the amplitude of the signal (i.e. of the waveform), ω is its angular frequency, and φ is the phase shift.

In doing computations involving such a waveform, we often need to multiply by constants, change the phase, and take derivatives and integrals, all of which often involves tedious manipulations of sines and cosines. The last two postings were perfect examples of this.

To simplify these calculations, the complex phasor was invented at the cost of making the calculations seem more abstract. To use complex phasors, a person replaces all sinusoids, such as cos(ωt + φ) , with a complex exponential of the form e^{i(ωt + φ)} . That is, we change Equation (1) into:

y(t) = A e^{i(ωt + φ)} . (2)

Technically, y(t) in Equation (1) is really just equal to the real part of Equation (2). However, the standard method is to temporarily set y(t) equal to the whole of A e^{i(ωt + φ)}, and only after we do all of our calculations and manipulations do we actually worry about taking the real part. This method seems to work just great as long as we never multiply two of of the time dependent complex exponential phasors together. In the last section, we saw an example of what happens if two time dependent complex exponential phasors are multiplied together ... we get the wrong answer.

To repeat some of the previous posting, in Table 1 we calculate the correct product of two signals using cosines, i.e. Equation (1) above. We show this product in Equation (1a) below. We also convert this correct product into its phasor form in Equation (1b) below. We then repeat the multiplication of the two signals using the complex phasors of the form of Equation (2) above. This second product (of phasors) is shown in Equation (1c) below. Equation (1c) does not equal the correct product in Equation (1b), illustrating that we cannot simply multiply two complex phasors together. To further illustrate the differences, the real parts of Equations (1b) and (1c) are graphed at the bottom of Table 1. for two different sets of parameters. We see that the two sets of graphs do not agree.

We have also include the result of the standard method for finding the average of two complex phasors multiplied together with graphs for this at the bottom of Table 1.

Table 1. Derivation of phasor products, correct and incorrect.

(1a)

Note that Equation (1a) is valid even in the case where A₁ and/or A₂ are exponentially decaying functions of time.

This is the exact cosine expansion we will be shooting for. We use the cosine identity:

(1a').

Note that (1a) contains a sinusoid at the sum frequency ω_s = ω₁ + ω₂ and another sinusoid at the difference frequency ω_d = ω₁ − ω₂ .

The phase sum φ_s and phase difference φ_d in (1a) are defined as φ_s = φ₁ + φ₂ and φ_d = φ₁ − φ₂

(1b)

We get (1b) by converting (1a) to complex phasor form. As we said above, we have a sum frequency and a difference frequency term.

(1c)

This is a simple minded expansion of the product of two complex phasors. You can see that it is not the same as (1b). It produces an incorrect result.

(1d)

This is the standard way of calculating the average of two complex phasors multiplied together. It involves taking the complex conjugate of the second phasor. When compared with Equation (1b), we see that Equation(1d) has the high frequency term e^{i(ω_st + φ_d)} averaged out, i.e. set to zero.

Looking at the bottom row of graphs just below, we see that these "averages" are not always even the averages you might expect. Particularly note the disparity between the first and third graphs on the left side.

	Graphs (below) for ω₁ = 100, ω₂ = 4, φ₁ = 0.3 , and φ₂ = 1.9 .	Graphs for ω₁ = 100, ω₂ = 90, φ₁ = 0.3 , and φ₂ = 1.9 .
Correct functions (at right), Eqn. (1b)
Incorrect functions, Eqn. (1c)
Averages of functions, Eqn. (1d)

A valid non-averaging method of multiplying two complex phasors

Basically this next method involves looking at the desired result, i.e. the final forms of Equations (1a) or (1b) above and using one of three ways to get there. These three variations are listed in the table which follows:

Table 2. Non-averaging methods of multiplying two complex phasors
1. Rule based variation: a. Express both phasors in polar form with a real amplitude and complex phase. b. The product will be of the form of Equation (1a) for the real form, OR c. Equation (1b) for the complex form.	Both the options, b and c, involve sum and difference angular frequencies and phases which are defined at the right of Equation (1a) above. The real amplitudes are multiplied together and divided by two as prescribed by Equation (1a).
2. One complex phasor and one real sinusoid: (2b)	In this variation we use one phasor in its complex form and one in its real sinusoidal form. It produces a complex phasor as an output. You can see from comparing the final form of Equation (2b) that this produces the same result as Equation (1b) above which used only real sinusoids. Thus this method produces correct results: it produces the correct complex product phasor.
3. Equation with complex conjugate: (2c) Comparing (2b) and (2c) with (1a) for the case where A₁ and/or A₂ are exponential decaying functions in time, we see that they all would produce the same result. This allows us to use (2b) and (2c) in the more general case where the phasors are of the form &psi = e^st where s is complex with real and imaginary parts. As with the rest of this posting, t is time.	In the work at the left, I have used the symbol ψ to represent a sinusoidal signal. This variation uses both phasors in their complex forms and uses the complex conjugate of one of them indicated by a bar over the ψ. Comparing the final form of Equation (2c) with Equation (1b) above we see that they are the same. Thus this method also produces correct results: it produces the correct complex product phasor. Note that the first line of Equation (2c) is not the equation sometimes used in quantum mechanics for the expectation value, nor the equation used in electrical engineering for the real part of the product. These other equations have an additional complex conjugate sign over the first ψ₁ on the right side of the first line.

Table 2. Non-averaging methods of multiplying two complex phasors

1. Rule based variation:

a. Express both phasors in polar form with a real amplitude and complex phase.
b. The product will be of the form of Equation (1a) for the real form, OR
c. Equation (1b) for the complex form.

Both the options, b and c, involve sum and difference angular frequencies and phases which are defined at the right of Equation (1a) above. The real amplitudes are multiplied together and divided by two as prescribed by Equation (1a).

2. One complex phasor and one real sinusoid:

(2b)

In this variation we use one phasor in its complex form and one in its real sinusoidal form. It produces a complex phasor as an output. You can see from comparing the final form of Equation (2b) that this produces the same result as Equation (1b) above which used only real sinusoids. Thus this method produces correct results: it produces the correct complex product phasor.

3. Equation with complex conjugate:

(2c)

Comparing (2b) and (2c) with (1a) for the case where A₁ and/or A₂ are exponential decaying functions in time, we see that they all would produce the same result. This allows us to use (2b) and (2c) in the more general case where the phasors are of the form &psi = e^st where s is complex with real and imaginary parts. As with the rest of this posting, t is time.

In the work at the left, I have used the symbol ψ to represent a sinusoidal signal. This variation uses both phasors in their complex forms and uses the complex conjugate of one of them indicated by a bar over the ψ.

Comparing the final form of Equation (2c) with Equation (1b) above we see that they are the same. Thus this method also produces correct results: it produces the correct complex product phasor.

Note that the first line of Equation (2c) is not the equation sometimes used in quantum mechanics for the expectation value, nor the equation used in electrical engineering for the real part of the product. These other equations have an additional complex conjugate sign over the first ψ₁ on the right side of the first line.

The above method used with complex amplitudes

While the methods discussed in Table 2 produce correct results, often it would be more convenient to allow the amplitudes A₁ and/or A₂ to be complex. In the context of a complex phasor, a complex amplitude contains both a magnitude and a phase shift in one compact complex constant. I will address this issue with regard to variations 2 and 3 in Table 2 first, and then go back to variation 1.

To find the effect of using complex amplitudes with the above methods, we will substitute amplitudes of the form (i.e. the polar forms):

and , (3)

where the tilde, i.e. the ~'s, over the amplitudes indicate that they are complex. The complex conjugate of these would add a minus sign in the exponent of e.

Table 3. Complex amplitudes
Desired result. (3a)	This is Equation (1b) from above, modified for complex amplitudes. The additional phase shifts of the amplitudes, the θ's, are added to the φ's. It is what we hope to achieve. The sum and difference phases of the amplitudes are defined in a similar manner to φ_s and φ_d from Equation (1a), i.e. θ_s ≡ θ₁ + θ₂ and θ_d ≡ θ₁ - θ₂ .
Variation 2 with complex amplitudes. (in Table 2) (3b)	This is incorrect. We see that the final result has a θ_s instead of the needed θ_d. However θ_s = θ_d if θ₂ = 0 . We conclude that we can use Variation 2 if the amplitude of the real sinusoidal phasor is real (as you might expect). So in the case that one phasor has a complex amplitude and one has a real amplitude, we should choose the one with the real amplitude to be the real phasor when we are using this variation.
Variation 3 using the complex conjugate. (3c)	We see that this produces the desired results. So Variation 3 from Table 2 is correct, even if the amplitudes are complex.
More on Variation 3. (3d) (3e) A little manipulation of Equation (3c) above yields this result. We see that this agrees with the conclusion next to Equation (3b) above, i.e that the real phasor needs to be totally real, having a real amplitude.	If we want to use Variation 3 with phasors having complex amplitudes, we would probably use the middle expression in Equation (3d), as is shown in Equation (3e). This method, Variation 3, is the recommended method if both amplitudes are complex.
Variation 1. Rule based method: a. Express one phasor in complex form (in polar and/or rectangular complex form). This phasor may have a complex amplitude. b. Express the other phasor in real sinusoidal form. The phase shift may be included in the argument of the sinusoid OR by having both sine and cosine terms (or some combination of these). This phasor may not have a complex amplitude. c. The product of these two phasors will yield the correct complex phasor form of the phasor product without averaging out the high frequency components.	Looking at Equation (3d), we see that Variation 3 is really just a restatement of Variation 2 involving one real phasor and one complex phasor. The rules we have given at left are a verbal statement of Variation 2, i.e. the beginning form of Equation (2b), and this is the rule based form of both Variations 2 and 3.

Various cases explored

Table 4. Various applications of the above methods
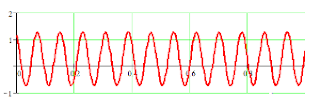
Case 1. Multiplication of two equal frequency phasors: (4a)	This is the result of Equation (3c) with ω₁ = ω₂ making ω_s = 2ω₁ and ω_d = 0 . We plot a typical time dependent power delivered to a complex load just below Equation (4a) for ω₁ = 40rad/sec and φ₁ = −0.4radians and φ₂ = 0.9rad . Note that the power pulsates, and is sometimes positive and sometimes negative. It is not centered on the x axis. Application: this equation is useful for calculating power delivered to a complex load as discussed in the last part of the previous posting. In that we gave a formula for the average power, i.e. ½I₀V₀cos(φ₁−φ₂). Note that if we strip out the high frequency part of Equation (4a) and take the real part of it, we are left with P_ave = ½I₀V₀cos(φ₁−φ₂), i.e. the same result. The advantage with using the methods on this page is that we also get the high frequency dependence, which was averaged out with the calculation on the previous page.
Case 2. Multiplication of two identical phasors, i.e. "squaring": (4b)	Here we replaced A₂ with A₁ and φ₂ with φ₁ in Equation (4a). Applications: this equation could be applied in a number of places in the previous postings to calculate energy and power.
Case 3. Calculating losses in an LRC resonator: (4c)	Here we calculate the time dependent power loss in a resistor in LRC decay, in the same vein as Table 2 of Section 2.6. We cannot use Equation (4b) because that is for a constant sinusoid, whereas here we calculate a squared phasor for a decaying sinusoid. However as explained in the dark red notes in Tables 1 and 2 above, we can uses our equations from Table 2 (and also those in Table 3 since they are based on Table 2 equations.) Using dq/dt from Table 6, Section 2.2, we write: where . Because we have complex amplitudes (s is complex) we chose to use the left form of Equation (3d) to calculate I². The rest is shown at the left and leads to Equation (4c). To check our result, we take the real part of Equation (4c) and compare this to Equation (2e) of Section 2.6. They are equal so we were successful. (Remember that Re(e^iωt) = cosωt while Re(ie^iωt) = −sinωt .) If you labored through the derivation in Table 6, Section 2.2, you will appreciate that the calculation here is considerably less work.

Table 4. Various applications of the above methods

Case 1. Multiplication of two equal frequency phasors:

(4a)

This is the result of Equation (3c) with ω₁ = ω₂ making ω_s = 2ω₁ and ω_d = 0 . We plot a typical time dependent power delivered to a complex load just below Equation (4a) for ω₁ = 40rad/sec and φ₁ = −0.4radians and φ₂ = 0.9rad . Note that the power pulsates, and is sometimes positive and sometimes negative. It is not centered on the x axis.

Application: this equation is useful for calculating power delivered to a complex load as discussed in the last part of the previous posting. In that we gave a formula for the average power, i.e. ½I₀V₀cos(φ₁−φ₂). Note that if we strip out the high frequency part of Equation (4a) and take the real part of it, we are left with P_ave = ½I₀V₀cos(φ₁−φ₂), i.e. the same result. The advantage with using the methods on this page is that we also get the high frequency dependence, which was averaged out with the calculation on the previous page.

Case 2. Multiplication of two identical phasors, i.e. "squaring":

(4b)

Here we replaced A₂ with A₁ and φ₂ with φ₁ in Equation (4a).

Applications: this equation could be applied in a number of places in the previous postings to calculate energy and power.

Case 3. Calculating losses in an LRC resonator:

(4c)

Here we calculate the time dependent power loss in a resistor in LRC decay, in the same vein as Table 2 of Section 2.6. We cannot use Equation (4b) because that is for a constant sinusoid, whereas here we calculate a squared phasor for a decaying sinusoid. However as explained in the dark red notes in Tables 1 and 2 above, we can uses our equations from Table 2 (and also those in Table 3 since they are based on Table 2 equations.)

Using dq/dt from Table 6, Section 2.2, we write:
where .

Because we have complex amplitudes (s is complex) we chose to use the left form of Equation (3d) to calculate I². The rest is shown at the left and leads to Equation (4c).

To check our result, we take the real part of Equation (4c) and compare this to Equation (2e) of Section 2.6. They are equal so we were successful. (Remember that Re(e^iωt) = cosωt while Re(ie^iωt) = −sinωt .) If you labored through the derivation in Table 6, Section 2.2, you will appreciate that the calculation here is considerably less work.