| All postings by author | previous: 3.16c Steady state response | up: Contents | next: 3.16e Smith chart |

3.16d - Transmission line resonators
Summary: Transmission line resonators find use in filtering and matching sections of high frequency circuitry as well as in common musical instruments such as flutes and organs. We mathematically explore the parameters of exciting transmission line resonators with waves on another transmission line.
Keywords: transmission line resonator, half wavelength resonator, Q0, loss in resonator
Topics covered in this posting
- Resonators made out of a length of transmission line instead of from components as in an LRC resonator.
- Derivation of the basic input impedance equation for transmission lines terminated in a load of specified impedance, in general and in the case of a lossless transmission line.
- Adjusting the parameters of an LRC circuit to best model a transmission line resonator.
- An equation for the unloaded Q of a transmission line resonator.

Contents
| 1. What is a transmission line resonator? | |||||||||
|---|---|---|---|---|---|---|---|---|---|
In addition to the LRC circuit resonators we have discussed earlier, sections of transmission lines can also function as resonators, analogous to organ pipe acoustic resonators; see [2nd reference] and [animations]. In fact Figs. 35 and 36 of an earlier posting show sections of acoustical transmission line functioning as resonators. Here we shall concentrate on one possibility, which most closely parallels the resonators in Figs. 35 and 36. Fig. 1 at right show an LRC resonator being driven by a transmission line. Figs. 2 and 3 show two similar circuits using transmission line resonators. We include the LRC circuit in Fig. 1 for comparison with the transmission line resonators of Figs. 2 and 3. Some simple equations for transmission line resonators. In Figs. 1 - 3, the AC voltage source V equals twice the actual incident wave amplitude, R0 = Z0 represents the characteristic impedance of the transmission line which we assume to be real (as opposed to complex). The coupling inductor LC allows some of the waves into the resonator. Figs. 2 and 3 show the resonator as a length of the same transmission line of length ℓ = λ0/2 = πc/ω0 where c is the speed of wave propagation in meters per second. The resistor RL on the far end of the resonator in Fig. 2 represents the internal loss element of the resonator. The internal loss element of the resonator in Fig. 3 is not shown but is assumed to be the distributed resistance and leakage conductance of the transmission line making up the resonator. Even though these losses are low, they can still play a very significant role in the resonator's operation because resonators typically "recycle" waves many times allowing small losses to add up to very significant losses. |
| 2. Input impedance, Zin | ||||||
|---|---|---|---|---|---|---|
a. Derivation of the basic equation Figs. 4 and 5, at right, show the setup for defining input impedance. The total wave impedance at the "point under investigation" in Fig. 4 is given by: where the above voltages and currents are measured at the "point under investigation". V+ and V− refer to voltages of the positive going and negative going waves respectively. We would like to use the reflection coefficient to relate the forward going wave to the negative going wave. This equation is: where Γ is the amplitude reflection coefficient. The problem with (3) is that the V+ and V− in this equation are the voltages of the positive and negative going waves at the load ZL, NOT at the point under investigation. On the other hand, we can use the propagation equation (Equation 12 of posting 3.20 to calculate the voltages at the point under investigation in terms of those at the load: where x = 0 denotes the location of the load impedance ZL while x = ℓ is the location of the point under investigation and ℓ is a positive number. For negatively propagating waves (4a) becomes: We combine (3), (4a) and (4b) to yield:
Equation (5) relates the negative going voltage at the point under investigation to the positive going voltage at the same point. 
We can now substitute (5) into (2) to solve for the input impedance: Note that the numerator and denominator are the same, except for the difference in sign between the two terms in each. Equation (6) forms the basis for the Smith Chart which is heavily used for transmission line calculations. We illustrate its use as applied to transmission line resonators in the next posting. b. Other forms of the input impedance equation Multiplying both the numerator and denominator of (6) by eγℓ and substituting the amplitude reflection coefficient equation Γ = (ZL − Z0) / (ZL + Z0) yields:
where γ is the complex propagation constant and we have used the complex hyperbolic trig definitions:
Substituting γ = α + i β into (7) yields:
where the hyperbolic trig functions of complex arguments can be evaluated using (8) or (10) below:
where z = x + iy is the complex variable and x and y are its real and imaginary parts [ref] see lines 4.5.49 and 4.5.50. c. Lossless case ( α = 0 ) Most practical transmission lines have low loss ( α = 0 ) and can be approximated as lossless for many calculations involving Zin. In this case (9) become much easier to evaluate. Setting α = 0 we see that (10) becomes:
which makes (9) become: Dividing both the numerator and denominator by cosβℓ we get: 
Equations (12) and (13) are both heavily used for calculating input impedance. (13) has the advantage of being a little simpler, while (12) avoids the singularity that (13) suffers from at βℓ = ±π/2, ±3π/2, ±5π/2, ... . To use (13) at these points, one needs to take the limit as βℓ approaches these values. One can also write these equations in a normalized form. When normalized, Eqn. (13) becomes: where ζL = ZL/Z0 and ζin = Zin/Z0 , i.e. all impedances are taken relative to the characteristic impedance of the transmission line, Z0 . |
| 3. Equivalence of various resonator models | ||
|---|---|---|
|
Figs. 1, 2 and 3 above show three different models for a transmission line resonator. We can use the above input impedance equations to figure out equivalence between these models. a. A lossless transmission line resonator We start with the lossless case for the transmission line circuits shown in Figs. 1, 2 and 3. The "lossless" case means that R in Fig. 1 is infinite and can be deleted so we are left with an LC resonator (and LC ) at the end of a transmission line. Similarly in Fig. 2, RL is also set to infinity and can be deleted making this circuit the same as that in Fig. 3. In Fig. 3 we only change the notation to reflect no loss in the resonator part of the transmission line. In the circuit in Fig. 1, we have a load impedance for the LC resonator given by: 
Similarly, using (12) with ZL approaching infinity, we find that the input impedance of the resonator part of Figs. 2 and 3 (remember they are the same circuit in the lossless case) is: where ω0 is the resonant frequency of the resonator by itself when the resonator part of the transmission line has a length ℓ = λ0 / 2 , i.e. a half wavelength. Thus in (16) we use the following two relationships:
We next work to get (16) in the same form as (15) by approximating the tangent around the point ω = ω0 :
We now approximate (15) as:
where in the second line of (19) we have approximated ω ≅ 1/√LC = ω0 . We see that (18) and (19) are identical if: These are consistent with what we have discussed in earlier postings. The second equation of (20) simply reaffirms the equation for the resonant frequency of an LC circuit. The first equation of (20) gives the characteristic impedance of an equivalent transmission line resonator. The two equations in (20) can be combined to solve for the values of L and C to make an LC circuit that is equivalent to our λ/2 transmission line resonator: Note that we used approximations to make the equivalence connection. This means that the tails of the resonance curve of the two circuits (Figs. 1 and 3 above) will differ, however the peak (or center) regions should be almost identical for the two circuits. Figs. 7, 8 and 9 plot the various approximations and demonstrate their validity in the center part of the resonance. 
b. Lossy case ( α > 0 ) i. Circuit of Fig. 2 compared with that of Fig. 1 We repeat the procedure from the lossless case, only this time including the loss elements. Equations (15) and (19) become:
With the addition of loss element R as in Fig. 2, equations (13) and (18) become:
where we have used the fact for our approximation that for reasonably high Q resonators, R must be chosen considerably larger than Z0 . We have also used the approximation for tanβℓ discussed for Eqns. (17) and (18) and Fig. 6 above. Equations (22) and (23) will be identical if conditions expressed in (20) and (21) hold, as well as the resonator resistors R in the two circuits (Figs. 1 and 2) are equal. One other point of interest is that the turquoise and blue lines of Fig. 11 are a Lorentzian function which is somewhat similar to a Gaussian function. Both functions are used in the study of statistically varying data. The Lorentzian also fits the observed frequency (or wavelength) absorption peaks of a gas due to collisions, while that due to Doppler broadening is Gaussian. We see from the above work that the electronic resonators studied here have an approximate Lorentzian resonance peak. ii. Circuit of Fig. 3 compared with that of Fig. 1 The losses in the resonator shown in Fig. 3 are totally contained in the transmission line itself. This means that the ZL in (13) will be infinite and the attenuation constant α is greater than zero. As discussed earlier this will affect the propagation constant γ but may or may not affect the characteristic impedance Z0 . It does mean that we need to use (9). Looking at (10) and assuming βℓ ≅ π , i.e. the half wavelength resonator approximation, we can approximate the following trig functions (shown in Figs. 12) as: sinβℓ = sin(πω/ω0) ≅ −(ω − ω0)/ω0 and cosβℓ = cos(πω/ω0) ≅ −1 . (24)
Assuming αℓ is small (low loss approximation) we can approximate (see Fig. 13): sinhαℓ ≅ αℓ and coshαℓ ≅ 1 . (25) Using (10) we get:
Using these with (9) and remembering that ZL is very large, we have:
where the second term in the numerator of the second step is small and is deleted in the final step. We repeat for comparison (22) from above (the approximate equation for the input impedance of a parallel LRC circuit): Equations (27) and (28) will be the same if: 
So we have the required R in our equivalent LRC circuit. Given the second part of (29) and the relation that ω0 = 1/√LC we can solve for the approximate required L and C in the equivalent LRC circuit: Since Q0 = R/ω0L for a parallel LRC circuit we get using (29) and (30): |
| 4. Q0 of a transmission line resonator |
|---|
Above we calculated Q0 of the transmission line resonator of Fig. 3 by the equivalent LRC circuit. We can also calculate Q0 by energy and power means. We do this for the circuits of Figs. 1, 2, and 3: a. Q0 of a parallel LRC circuit as in Fig. 1 above
where the last two expressions are equivalent and are related by ω0 = 1/√LC . We wrote U (the energy in the resonator) and P (the power dissipated by the resonator) in terms of the magnitude of the voltage (instead of current) because all three circuit elements in a parallel LRC circuit see the same voltage. The ½ in the numerator is part of the basic equation for the energy in a capacitor, that during the resonant cycle flows back and forth between the capacitor and inductor but is entirely in the capacitor when the voltage peaks, i.e. equals the voltage magnitude. The ½ in the denominator comes from averaging the power dissipated by the resistor: it equals |V |2 at the cyclic voltage peaks and equals 0 when the voltage is zero and averages ½|V |2/R . b. Q0 of the resonator in Fig. 2 above
where most of the comments following (32) above hold. V is the voltage across the resistor RL, at the very end of the transmission line. The additional ½ in the numerator is due to spacial averaging. That is: at resonance the voltage of the standing wave is not uniform but instead peaks at the two ends and is zero at the midpoint. The average energy in the capacitance of the transmission line is (½)(½)|V |2C1ℓ . The factor C1 is the capacitance per unit length of the transmission line and ℓ is its length. We can rewrite (33) in terms of more common transmission line parameters using the following equations: where lower case c is the speed of wave propagation on the transmission line. These equations assume no or low loss in the transmission line itself. Remember that for this circuit (shown in Fig. 2 above) that we assume that all the losses are due to the resistor RL. Together, these can be solved for L1 and C1: The length of the half wavelength transmission line resonator is given by: The Q0 of the transmission line resonator is now: c. Q0 of the resonator in Fig. 3 above
where G1 is the conductance per unit length between the conductors of the transmission line. R1 is the resistance per unit length of the transmission line. Equation (38) assumes a high Q0 (low loss) so that the standing wave pattern inside the resonator is not appreciably changed by the losses in the transmission line. That is to say, we assume that U = (½)(½)|V |2C1ℓ is the correct expression for the energy in the transmission line and P = (½)(½)|V |2G1 + (½)(½)|I |2R1 is the correct expression for the average dissipated power. A high Q0 will also mean that |Z0|2 can be approximated by (34) above and will be real so that (38) becomes: d. Does (39) agree with (31) above?
Equation (31) is written in terms of the attenuation constant α . For small losses ( R1 << ω0L1 and G1 << ω0C1 ) we can approximate α as:

where we have used the right expression in (34) for the speed of the waves, c . We now substitute (40) and (36) into (31) and clean up the result a little with the left side of (34) to arrive at (39):
which is the same as (39). |
| All postings by author | previous: 3.16c Steady state response | up: Contents | next: 3.16e Smith chart |











 . (5)
. (5)

 , (7)
, (7) . (8)
. (8) , (9)
, (9) , (10)
, (10) , (11)
, (11)







 . (18)
. (18)
 . (19)
. (19)




 . (22)
. (22)







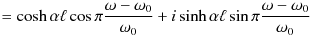
 , (26a)
, (26a)

 . (26b)
. (26b) , (27)
, (27)
















 , (38)
, (38)
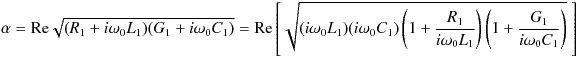
 , (40)
, (40) , (41)
, (41)