Resonances, waves and fields: Energy in a resonator

This posting includes a flash animation showing the physics discussed. Most computers have a flash player already installed, but if yours does not, download the free Adobe flash player here.

Figure 1. Decay of water level in a leaking reservoir. Click on the figure to start or restart it. Mousing off and on again will stop and restart the animation.
The pressure forcing the water out through the shower head is proportional to the depth of water in the reservoir. This means the rate of water loss from the reservoir is proportional to the depth. Thus as the water level drops, the pressure drops, the water flow decreases, and the water level drops less and less rapidly. In the left side of the graph, the depth and pressure is greatest, so that the rate of decrease (or slope) is the greatest. At the right side, the depth and pressure is smallest and the rate of decrease (slope) is almost zero.

To put this into an equation, the rate of water loss is proportional to the amount of water in the container:
           R = αV  ,       (1)
where R is the rate of water loss (liters per second), α is the proportionality constant, and V is the volume of water in the container. We also know that the rate of water loss equals the rate of water decrease in the container:
    −dV/dt = R = αV   .  (2)
Simplifying, we get:
    dV/dt = −αV   .     (3)
This has the standard solution of:
    V = V₀e^−αt   ,       (4)
where t is time and V₀ is the initial volume of water (at t = 0).

2.5 Energy in a resonator, shock excitation

In the previous posting, we considered the internal workings of a resonator looking at the interactions of force and momentum in a lossless resonator. We also discussed the interplay of potential and kinetic energy. In this and the next posting, we look at the relationship between energy and power loss in a lossy resonator having been shock excited.

When we shock excite a resonator, we very quickly fill the resonator with a certain amount of energy. This energy rattles around inside the resonator, oscillating in its form, as we discussed in the last posting. In contrast to our discussion in the last posting, in all real resonators there are losses and these losses cause the energy to decay in time, similar to what we saw with respect to the amplitude of the oscillations of the parameters in part 2.1 .

The decay of energy in a resonator is similar to the fall of the water level in a leaky bucket. We animate this at the right, where the "leak" is the water going into a shower head. As we see there, the water level undergoes an exponential decay similar to the envelope in the earlier posting.

Power loss

A resonator's power loss is defined as the rate of energy loss:

P = −dU/dt , (5)

where P is the power loss and U is the energy in the resonator. The minus sign is used to make the power loss a positive quantity.

For most resonators, the power loss is proportional to the energy contained in the resonator:

P = αU , (6)

where α is the proportionality constant. We should point out that Equation (5) is just approximately true, that power loss is often proportional to kinetic energy and not to the total energy. We shall explore this distinction more in the next section, with the LRC circuit resonator.

Equating the power in Equation (5) with that in Equation (6), yields:

dU/dt = −αU . (7)

This is in the form of a standard first order differential equation that governs many phenomena in technology and science (for an example, see Figure 1 above or here or here).

Equation (7) has the standard first order differential equation solution:

U = U₀ e^−αt , (8)

where t is time and U₀ is the initial energy in the resonator, i.e. the energy at t = 0.


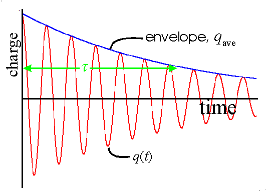
Figure 2a. LRC circuit.	Figure 2b. Decay of oscillations in the LRC circuit in response to shock excitation (such as a voltage spike).

Equation (8) has the form of an exponential decay. We discussed exponential decay earlier with respect to the decay of oscillating parameters in resonators. We next do a more careful analysis on one particular resonator, the LRC circuit resonator, for which we have derived equations in the previous postings.

Energy in an LRC circuit resonator

In sections 2.1 and 2.2 we derived the time response to a shock excited LRC circuit resonator, shown in Figure 2a, at right. We see the result of these calculations in Figure 2b, along with the envelope (in blue) of these oscillations. Next we use these results to calculate the energy in the LRC circuit as a function of time. The energy is stored in the inductor and capacitor and flows back and forth between them.

Table 1. Derivation of energy in a shock excited LRC resonator.
(1a)	This is the standard equation for the energy stored in an inductor. (This is analogous to the kinetic energy in a moving mass, i.e. ½ mv² = ½ m(dx/dt)² .)
(1b)	This is the standard equation for the energy stored in a capacitor. (This is analogous to the potential energy in a spring, i.e. ½ kx² .)
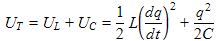(1c)	The sum of the Equations (1a) and (1b) above gives the total energy stored as a function of time. We next go back to Equations (3b) and (4a) of section 2.1 to get the equations for q(t) and dq(t)/dt for an LRC resonator.
(1d)	This is a copy of Equation (3b) from section 2.1 that gives the charge on the upper plate of the capacitor as a function of time.
(1e)	This is a copy of Equation (4a) from section 2.1 that gives the first derivative of q(t) .
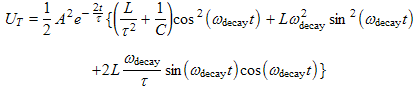(1f)	Here we show the substitution of Equations (1d) and (1e) into Equation (1c). We have factored out the common factors and put these at the beginning. Most of the complication comes from having to square dq/dt. The complex methods would fail us here if we want anything except the energy averaged over one cycle. Complex methods can be tricky when the oscillating variables are squared.
where , , 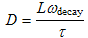(1g)	We use two trigonometric identities. sin²θ = 1 − cos²θ changes the sine squared term into a cosine squared term (plus a constant). We also use sinθ cosθ = ½ sin2θ .
(1h)	We use the trigonometric identity cos²θ = ½ cos2θ + ½ to further simplify the cosine squared term in Equation (1g). We also used Equations (4a) and (4b) from section 2.1 to show that . Equation (4b) of that previous section also implies that 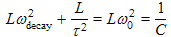which we also used to simplify this expression.
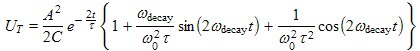(1i)	Here we have used τ = 2L/R and ω₀² = 1/LC from section 2.1 to change the previous equation into a form that is more universal to all resonators. For longer lived resonators where ω₀τ≈ω_decayτ>>1, the first terms inside the braces (the "1") dominates and the energy decay is fairly smooth, similar to that shown in Figure 5 above. In this case the ripple is small.
(1j)	This is an alternate form of Equation (1i) in the form of an amplitude and phase shift instead of using both sine and cosine terms. The phase shift arctan(1/ω_decayτ)≈1/ω_decayτ is also small and the oscillating term inside the braces is approximately given by [sin(2ω_decayt+1/ω_decayτ)]/ω₀τ .

decaying oscillations of an LRC resonator

Figure 3a. Charge graphed as a function of time for an LRC circuit resonator.

Figure 3b. Energy graphed as a function of time for an LRC circuit resonator. Note that the time constant (shown in green) for energy decay is half the time constant for the decay of the charge oscillations shown in Figure 3a. Note also that the red energy decays in ripples. The blue curve is the same function without the ripple (an average of sorts), i.e just the "outside multiplier" ½(A²/C)e^−2t/τ.

Whew! The details of the derivation of Equation (1i) are quite involved ... a lot of algebra! Having put in the effort, we should study our results some.

First, the energy from Equation (1i) is graphed at right in Figure 3b. We see a ripply decay, as opposed to the simple smooth exponential decay discussed earlier.
Equation (1i) has an outside multiplier, . This factor is the source of the exponential decay of all the terms inside the bracket.
When compared with the exponential decay of the oscillating parameters (discussed in section 2.1) we see that e is raised to a power of −2t/τ instead of −t/τ as with the oscillating parameters. Thus the exponent in the power decline has an extra "2" in it. This makes the decay of energy occur twice as fast as the oscillating parameters. A simple explanation of this is that the energy is proportional to the oscillating parameters squared and this "square" makes the "2" and leads to the faster decay. We can also say that effectively the energy decays with a time constant τ_energy = ½ τ where τ is the decay time constant for the oscillating parameters.
Inside the brackets of Equation (1i), we see a constant term and two double frequency terms, one a cosine and one a sine. The constant term, when multiplied by the outside multiplier just discussed, produces the exponential decay that would be a smooth decay if it were not for the double frequency sinusoids.
The two double frequency sinusoids are responsible for the ripple. The two work together to allow for a phase shift of that ripple.
It is easy to understand the reason behind the ripple. The loss of energy (power loss) is proportional to the current squared flowing through the circuit (specifically, through the resistor). Stated another way, the loss is proportional to the kinetic energy in the resonator and varies as the kinetic energy varies. Thus we would expect to see the energy decline when the kinetic energy (or current squared) peaks, and see very little decline when the kinetic energy is minimal. Thus instead of a stead decline in energy, we expect (and see) a decline that pulsates as the current pulsates.
Could we arrange for the energy to decay in a smooth exponential? Yes, if the power loss were made to be proportional to the right mix of both current squared through the circuit (as it is above) plus the voltage squared across the capacitor, as it might be if we used a leaky capacitor or if the proper additional resistor were placed in parallel to the capacitor.