Origins of Newton's laws of motion

Origins of Newton's laws of motion

Fig. 1. Sir Isaac Newton.

Newton's laws of motion are central to our society's ability to design and build things that move, e.g. aircraft, cars, ships, rockets, turbines, hard disk drives, etc., a lot of our modern technology. Newton's laws have even been applied to the motion of people and ancient dinosaurs. The three laws of motion were published in 1697 over three centuries ago.

How did Newton come up with these famous laws?

Actually Newton did not discover his laws in isolation. Many people were involved with coming up with pieces of the laws which Newton put together and verified. This posting lists the more famous of these earlier scholars. There are many more not quite so famous. It may be surprising that the quest had mostly to do with our understanding of how the planets in the solar system move ... that mankind figured out how objects move on Earth by studying how planets move in space. Furthermore, we were able to do this without modern technology.

Fig. 2. Roman copy of an old Greek bust of Aristotle by Lysippos from 330 BC.

Fig. 3. A 16th century rendition of Ptolemy's model of the universe showing the Earth at the center with all other heavenly bodies orbiting around the Earth.

Historical people in the quest to uncover the laws of motion:

• Aristotle 384-322 BC: We begin with Aristotle 23 hundred years ago. This philosopher of ancient Greece wrote about many things. Concerning motion, he stated that objects in this world tended to return to their native state which he deemed was at rest. According to Aristotle an object will continue to move only if there is an active force continuing to push it it, otherwise it would return to its rest state of not moving. Aristotle was a believer in observing the world around him and this was certainly what he observed in the world as a human, that moving objects naturally come to rest.

  While a few other thinkers argued against this, Aristotle's teachings were generally accepted as the truth for the next 15 hundred years.

• Claudius Ptolemy 90-168 AD: A member and astronomer of the Egyptian ruling class. He used old Babylonian astronomical data as well as his own measurements of stars and planets to create convenient tables which allowed a person to compute past and future positions of the planets. He viewed the universe as a set of nested spheres, each containing a planet, the Sun, the Moon or the fixed stars. The Earth was at the center of his model and did not move, while the rest of the heavenly bodies rotated around the Earth, all at different speeds and each with its own specific oddities. Like Aristotle's teachings, Ptolemy's solar system model was accepted as the truth by the western world for many, many centuries.
• Nicolaus Copernicus 1473-1543: - Mathematician and astronomer of Prussia (now Poland) created a model of the universe with the Sun at its center. His famous book was published in 1543 after his death, De revolutionibus orbium coelestium (On the revolutions of celestial bodies). His model was based largely on Ptolemy's data with Copernicus adding 27 observations of his own. His model showed everything except the Moon going around the Sun in perfectly circular orbits. While his model made it much easier to understand the complicated motions of the planets, it required the Earth to be moving, an idea that the common man and the church found hard to accept.

  There is no one center in the Universe. The Earth's center is not the center of the Universe. The center of the universe is near the Sun. The distance from the Earth to the Sun is imperceptible compared with the distance to the stars. The rotation of the Earth accounts for the apparent daily rotation of the stars. The apparent annual cycle of movements of the Sun is caused by the Earth revolving around it. The apparent retrograde motion of the planets is caused by the motion of the Earth from which one observes.

  Fig. 4. Copernicus' vision of the universe in De revolutionibus orbium coelestium.

  Fig. 5. Main tenets of Copernicus' model of the universe.

  
  

  Fig. 6. Geo-heliocentric model of the universe (1573) - final model espoused by Brahe.	Fig. 7. Mural quadrant (1598). One of the instruments to measure star and planet positions by Tycho Brahe.

  
  
• Tycho Brahe 1546-1601: A nobleman/astronomer in Denmark (currently Sweden) who is famous for his comprehensive and accurate measurements of planet and star positions over a 20 year period. His very precise and thorough measurements provided the data for later breakthroughs. Even though he never believed Copernicus' heliocentric model, Brahe's final model of the solar system was very close to that of Copernicus.
• Johannes Kepler 1571-1630: German mathematician, astronomer and astrologer. His life was filled with hardships: deaths of loved ones and a lack of money. At some point he started working for Brahe and was given complete use of Brahe's data upon Brahe's death. After ten years of working on the data, Kepler published Astronomia nova (a new astronomy) in 1609 in which he formulated three laws of planetary motion. In doing so he distilled Brahe's voluminous data into a brief but accurate geometric and mathematical description of the orbits of planets around the Sun.

  The orbit of every planet is an ellipse with the Sun at one of the two foci. A line joining a planet and the Sun sweeps out equal areas during equal intervals of time. The square of the orbital period of a planet is proportional to the cube of the semi-major axis of its orbit.

  Fig. 8. Kepler's three laws of planetary motion.

  Fig. 9. Illustration showing the orbit (gray ellipse) of a planet around the Sun (in yellow) according to Kepler's first and second laws. The time it takes for the planet to move from point a to point b is equal to the time it takes it to move from point c to point d. The areas (shown in blue) are equal. In order to better show the concept, this illustration has an exaggerated ellipse. Real planetary orbits are closer to circular.

  
  

  Fig. 10. Galileo showing his telescope to nobility.

  Fig. 12. Christiaan Huygens.

  Fig. 13. Reflecting telescope invented and made by Newton.

• Galileo Galilei 1564-1642: Italian physicist, mathematician, astronomer, and philosopher, supporter of Copernicus' and Kepler's work. Developed and tested the idea that an object in motion stays in motion without outside forces. For this he used balls rolling down inclined planes. Because of the Earth's curved surface he erroneously believed that planetary elliptical tracks were the natural unforced continuation of their motion not requiring any force. He also used a telescope, which he invented, to observe mountains on the Moon suggesting to him that the Moon was made of similar stuff as the Earth and would similarly have inertia.

  Fig. 11. Statue of Descartes.

• Rene Descartes 1596-1650: French philosopher, mathematician and writer who developed Cartesian coordinates and put together work by others to develop modern algebra.
• Christiaan Huygens 1629-1695: Dutch astronomer, physicist, probabilist and horologist (expert on clocks). While he developed many important ideas of today's physics, with regard to the laws of motion he derived the formula for centripetal force which arises in circular motion F = mv²/r . This formula was essential to Newton's developing his laws of motion and gravity.
• Isaac Newton 1643-1727: English physicist and mathematician. Published Philosophiæ Naturalis Principia Mathematica (Mathematical Principles of Natural Philosophy), in 1687 explaining his famous laws of motion. Newton was first to develop a set of mathematical laws or equations for the motion of all objects from planets down to those in ordinary human life. His laws also included a law of gravity. He developed calculus which he used to apply his laws of motion and gravity to explain the orbits of planets, their moons, and comets. [Mathematician Gottfried Wilhelm Leibniz also developed calculus simultaneous to Newton. Leibniz's notations for calculus are still in use today.]

Fig. 14. Diagram of Copernicus' heliocentric solar system. The Sun is shown at the center with the orbits of the known planets. The Earth has the circular orbit of the Moon around it.

Fig. 15. Galileo's inclined plane experiments. He determined that if the friction is reduced sufficiently, a rolling ball will lose very little of its momentum and will coast up a second inclined plane to the same height as it started with on the first inclined plane.

The major pieces:

The major threads of thinking that went into the laws of motion were:

1. Understanding the orbits of the heavenly bodies in a simple model that is capable of being explained with just a few laws of motion.

   With regard to understanding the motions of the heavenly bodies, Ptolemy started the effort. Copernicus' insight was a tremendous leap forward. Using Brahe's data, Kepler confirmed and extended Copernicus' model.

2. Understanding the natural undisturbed state of a moving object: without outside forces, will a moving object "return" to a motionless state or will it continue to move with its initial velocity?

   With regard to understanding the undisturbed state and inertia, Aristotle set the stage. Galileo experimentally showed Aristotle to be in error and showed that without an outside force, moving objects will stay in motion. Descartes (and others) modified Galileo's insight with the idea that a moving object without any external force will continue to move in a straight line and not a curve as Galileo assumed. This meant that a force would be required to make a planet orbit around the Sun as derived by Huygens. Using his invention, the telescope, Galileo observed mountains on the Moon suggesting that the Moon and other heavenly bodies were massive like the Earth and had inertia.

   One of the problems facing the early scholars involved the poorly differentiated concepts of weight, mass, inertia and momentum. Even today, the word "inertia" can refer to either the mass of an object or to its momentum (the mass times the velocity) and is not considered a precise word to use by physicists. Even so, "inertia" (or "impetus", its equivalent at the time) with its built-in ambiguity seemed to be the word that the old scholars often used in discussions of the motion of objects. Because of the ambiguity, in his Principia Newton carefully coined the word "mass" to refer to the mass of an object (separate from its weight), and used the term "quantity of motion" to refer to its momentum. The word "momentum" was coined later (perhaps in 1720 by Jennings).

   Fig. 16. Descartes put together and used modern algebraic concepts.

3. Developing the mathematical machinery required for the application of the laws of motion to explain planetary motion, as well as the motion of objects in our everyday lives. Many mathematicians around the globe developed parts of algebra, but perhaps Descates was first to put it all together. Newton invented calculus to allow him to apply his laws of motion to the orbits of the planets.

Newton puts the pieces together in his laws:

Fig. 17. Sir Isaac Newton.

Fig. 18. Cover of Newton's Principia. This book was instantly a hit in Europe.

Fig. 19. Newton's first law of motion says that without external forces, like friction, a moving object will continue moving forever.

Like most great thinkers, Newton assembled his laws from insights of other thinkers, then extended and verified them. Below are his three laws of motion plus his "universal law of gravity". All four of these were revealed in his Principia. In this book, Newton provides great numbers of geometry proofs of various assertions and validations. He shows that these laws would cause the planetary orbits as specified by Kepler, as well as other effects that we observe in the world around us.

Law 1: Every object in a state of uniform motion tends to remain in that state of motion in the same direction unless an external force is applied to it.

This is really a restatement of Galileo's law of inertia with the modification that an unforced moving object will continue on a straight line and not on a curved path.

---

Law 2: The force required to change the momentum of an object (mass times its velocity) is equal to the change in momentum per unit of time. This law is usually remembered as F = ma , i.e. force equals mass times acceleration.

Fig. 20. Newton's second law states that the force required for an acceleration a is equal to the accelerated object's mass m times the acceleration, i.e. F = ma where the force is in the same direction as the desired acceleration.

This is a quantitative extension of the concept in Law 1, i.e. Law 1 addresses the no-force case and Law 2 addresses the force case. Certainly all the scholars who would agree with Law 1, such as Galileo, had in their mind that a force was required to make an object deviate from a constant velocity path. A lot of the problem was that the instrumentation to measure trajectories and forces with reasonable precision was lacking at Newton's time. However, because of the fascination of scholars over the centuries with the the motion of heavenly bodies, the planetary trajectories were precisely known and the force required to keep them in these trajectories also was almost figured out.

Building on Huygens centripetal force, a number of scholars had reached the conclusion that the Sun would need to attract a planet with a gravitational force inversely proportional to the planet's distance to the Sun squared in order to cause the elliptical orbits that Kepler had discovered. It apparently made sense to Newton that such a force would also need to be proportional to the planet's mass so that very heavy planets would experience greater force and so be pulled into similar elliptical orbits as lighter ones.

Newton painstakingly verified that this gravitational force along with his Law 2 would produce the motion of the planets as specified by Kepler. A modern derivation of Kepler's laws from Newton's laws is found here.

Fig. 21. Illustration of Newton's third law and his law of universal gravity. Note that the force exerted on mass 1 is the same magnitude as that on mass 2 but opposite in direction.

---

Law 3: For every action there is an equal and opposite reaction. This means that if one object exerts a force on a second object, the second object will automatically exert an opposite force on the first object. The "opposite force" will be exactly equal in magnitude to the first force, but exactly opposite in direction. This means that a force should be considered a symmetrical interaction between two objects rather than one object affecting the other.

At the time of Newton's work John Wallis had already verified that momentum was conserved during a collision. In order for Newton's dynamics to be consistent with momentum conservation, this third law was required. It also was consistent with and suggested by the symmetrical nature of Newton's gravitational force equation.

Fig. 22. Cavendish's balance. This extremely sensitive instrument was able to accurately measure the very weak gravitational force between two weights brought near each other, the force predicted by Newton's equation for gravity.

Fig. 23. Newton's drawing of the orbit of Halley's comet showing the orbit and blown out tail of the comet, as well as the Earth's orbit (G-H). The Sun (not shown) is at the point labeled "D".

---

Law of gravity: (Partially discussed above with respect to Law 2.) All objects exert attractive gravitational force on all other objects. In the case of two objects this force is proportional to the product of the masses of the two objects and inversely proportional to the distance between their centers squared. The force on each object is directed towards the center of the other mass.

Today this law is written as F = Gm₁m₂ / r² where G is the gravitational constant. G was initially measured by Henry Cavendish in 1796 and currently is accepted as 6.67×10^-11 N·(m/kg)².

As mentioned above under Law 2, a number of scholars of and prior to Newton's time had reached the conclusion that the "gravitational" force the Sun exerts on a planet must be inversely proportional to the planet's distance to the Sun squared. Adding a proportionality to the mass of the planet just made common sense.

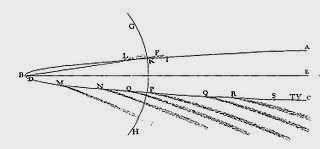
Newton's genius shone when he concluded that perhaps this gravitational force existed between all objects not only between the planets and the Sun. Thus it would apply to the force between the Earth and the Moon, between the Earth and a comet and between the Earth and terrestrial objects. To make the force equation universally applicable, he also (correctly) guessed that the force must be proportional to the masses of both objects involved. In the case of a planet and the Sun, it would thus be proportional to the masses of both the planet and the Sun. He carefully verified that his laws explained the observed orbit of Halley's comet.

References:

1. Numerous sites on Wikipedia e.g. under Newton's laws, Isaac Newton, and the various other people mentioned above. Most sites are linked in the text. Many of the above illustrations are courtesy of Wikimedia.
2. The Scientists, John Gribbin, Random House, NY, 2002.
3. Isaac Newton, James Gleick, Pantheon Books, NY, 2003.

All postings by Author