There are all sorts of resonances around us, in the world, in our culture, and in our technology. A tidal resonance causes the 55 foot tides in the Bay of Fundy. Mechanical and acoustical resonances and their control are at the center of practically every musical instrument that ever existed. Even our voices and speech are based on controlling the resonances in our throat and mouth. Technology is also a heavy user of resonance. All clocks, radios, televisions, and gps navigating systems use electronic resonators at their very core. Doctors use magnetic resonance imaging or MRI to sense the resonances in atomic nuclei to map the insides of their patients. In spite of the great diversity of resonators, they all share many common properties. In this blog, we will delve into their various aspects. It is hoped that this will serve both the students and professionals who would like to understand more about resonators. I hope all will enjoy the animations.

For a list of all topics discussed, scroll down to the very bottom of the blog, or click here.

Origins of Newton's laws of motion

Non-mathematical introduction to relativity

Three types of waves: traveling waves, standing waves and rotating waves new

History of mechanical clocks with animations
Understanding a mechanical clock with animations
includes pendulum, balance wheel, and quartz clocks

Water waves, Fourier analysis


Thursday, July 7, 2011

Mathematical derivations of special relativity - introduction


all topics by author introduction to relativity contents of mathematics of relativity next: Electromagnetic wave equation from Maxwell's equations

All topics by author

Introduction to relativity:

Math of relativity

1. Introduction

a. Flowchart of the math

Lorentz's logic:

2. Electromagnetic wave equation from Maxwell's equations

3. Invariance of the wave equation

4. Inverting Lorentz transforms

5. Length contraction and time dilation from Lorentz transforms

6. A constant speed of light from Lorentz transforms

Einstein's logic:

7. Length contraction and time dilation from a constant speed of light flash animations

8. Lorentz transforms from length contraction and time dilation

Equations shared by both Einstein and Lorentz:

9. Velocity transforms

10. Relativistic mass

11. Relativistic kinetic energy

12. Electromagnetic fields-intro and contents

13. Transforming charge and current densities

14. Four-vectors

15. Electric and magnetic field transforms

Rechecking the invariance of Maxwell's equations:

16. Transforming Maxwell's equations-intro and 1st ME

17. Transforming Maxwell's equations 2, 3 and 4

18. Separating the transformed Maxwell equations

19. References

This section involves a number of mathematical derivations. They are meant to show the underpinnings of relativity, both from Einstein's point of view and Lorentz's point of view. There is an outline of the various chapters at the right and a flow chart of the logical progression of the chapters at the bottom of this posting. If you are interested in a non-mathematical treatment of relativity which stresses the history, the phenomena, and philosophy, see my earlier introduction to relativity.

Einstein's view was that all of relativity flows from the truth that physics should look the same in all inertial reference frames (reference frames traveling at constant velocity). This means the speed of light is the same, and all basic equations of physics are the same in all inertial reference frames.

Lorentz's point of view was that the above consistency was simply an illusion that was made possible by an oddity in Maxwell's equations. His view was that the speed of light and the equations of physics really differ in different inertial reference frames. However, people and their instruments in these frames are affected in such a way as to make the speed of light and the equations of physics seem the same. Furthermore, he felt that there probably is a true "at rest" (or universal) reference frame, but as yet we do not know how to ascertain which reference frame that is. This would be perhaps like the early chemists (Boyle, Lavoisier, etc.) who didn't have a chance of directly verifying the existence of atoms or molecules, but still correctly used atoms and molecules as central entities in their theories.

As was explained in the previous postings, the two views are mathematically identical and barring any future discovery, we may never know which is really "correct". In any case, in this section we present the mathematics behind relativity.

For the most part, the mathematics in the following postings follow the standard relativity derivations, i.e. they follow Einstein's logic: starting with a constant speed of light and going on to derive transformations between reference frames for all sorts of physical quantities.

In addition to the standard logical progression, we include a few derivations, at the very beginning, supporting Lorentz's views. These derive the electromagnetic wave equation from Maxwell's equations to illustrate the lack of reference frame in the wave equation. We go on to show that the electromagnetic wave equation is not invariant under the old Galilean velocity transforms, but it is invariant under Lorentz transformations. We also discuss the implications of this from Lorentz's point of view.

To some extent, the chapters can be read individually to suit one's interest. For example, people interested primarily in the conventional Einsteinian logic might be mostly interested in reading Chapter 7 and a few chapters thereafter.



Flowchart for the math of relativity
mathematics of special relativity - flow chart
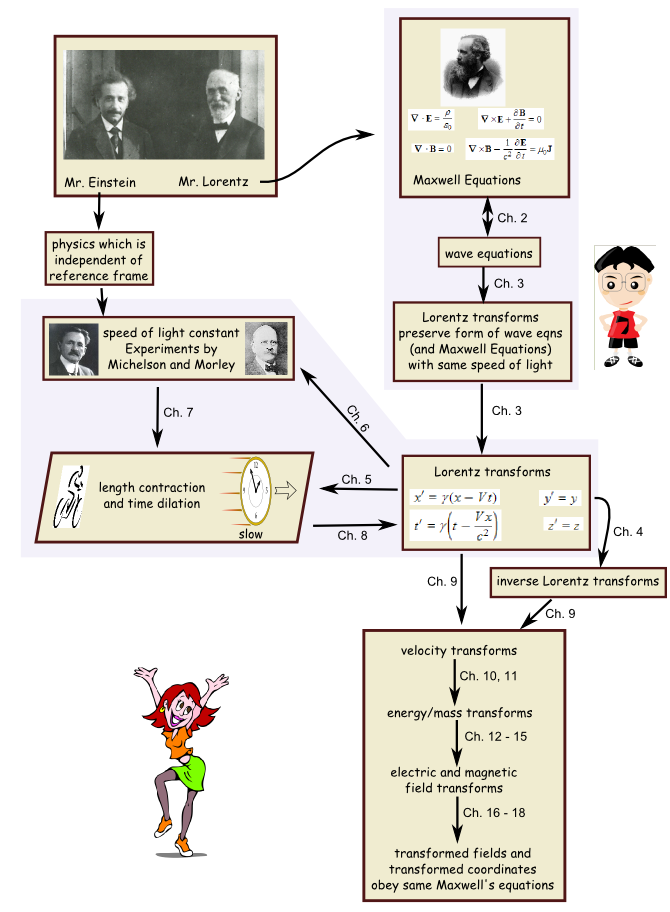
Fig. 1.1. This illustration shows the logical flow of this math section: which chapter shows which relationship.


all topics by author introduction to relativity contents of mathematics of relativity next: Electromagnetic wave equation from Maxwell's equations

Posted by P. Ceperley at 10:43 AM