17. Transforming the second, third and fourth Maxwell equations
Transforming the second Maxwell equation
We start transforming the second Maxwell equation. This is a vector equation:

|
Because of its complexity, we now finish the transformation component-by-component:





|


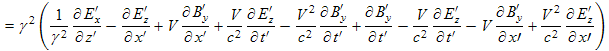



|
Note that 1/γ2 = 1 − β2 where β = V/c (see the definition of γ ).



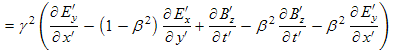

|
Transformation of the third Maxwell equation
The third Maxwell equation transforms similarly to the first one above:
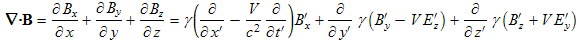
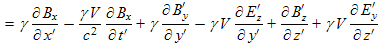

|
Transformation of the fourth Maxwell equation
The fourth Maxwell equation is a vector equation and will transform in a similar manner to the second Maxwell equation above. We start by transforming the left side of the fourth Maxwell equation:

|
Now we transform this component-by-component:


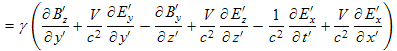



|
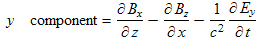
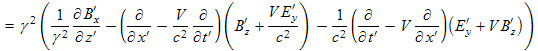

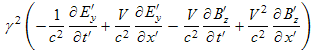


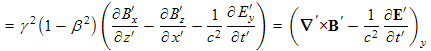
|


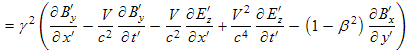



|
The right side of the fourth Maxwell equation is transformed as:

|
where we have used the relation: c2 = 1/(ε0μ0 ) which can be solved for μ0, i.e.: μ0 = 1/(c2ε0) .
Combining the above equations, we get:

|