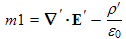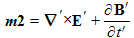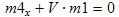18. Separating the transformed Maxwell equations
In Fig. 18.1 below, we restate the transformed Maxwell Equations as derived in the previous two chapters:
| The first Maxwell equation as transformed: Chapter 16, Fig. 16.5 |
| The second Maxwell equation (a vector equation) as transformed: Chapter 17 |
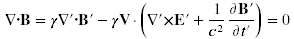
| The third Maxwell equation as transformed: Chapter 17 |
= 0 | The fourth Maxwell equation (a vector equation) as transformed: last equation in Chapter 17 |
| Fig. 18.1. Transformed Maxwell Equations as derived in the previous two chapters. | |
Unfortunately Maxwell's equations transformed as mixes of Maxwell's equations in the prime reference frame. We now need to separate the mixes. In order make the equations more manageable, we will use the abbreviations shown below in Fig. 18.1a. Note that each of the newly defined quantities are the left sides of the wished for Maxwell equations in the primed frame. We hope to show that the above equations (in Fig. 18.1 above) imply that all these quantities listed in Fig. 18.1a are zero.
| Definition of m1, equal to the left side of the first transformed Maxwell equation. |
| Definition of the vector m2, equal to the left side of the second Maxwell equation (a vector equation). |
| Definition of m3, equal to the left side of the third Maxwell equation. |
| Definition of the vector m4, equal to the left side of the fourth Maxwell equation (a vector equation). |
| Fig. 18.1a. Definitions of variables used to separate out and isolate the various Maxwell equations. | |
Using the definitions in Fig. 18.1a, we can be expressed the equations in Fig. 18.1 as:
(C1)
| The first Maxwell equation as transformed written in terms of m1 and m4x. |
(C2x)
(C2y)
(C2z)
| The second Maxwell equation (a vector equation) as transformed and written in terms of the variables m2 and m3. |
(C3)
| The third Maxwell equation as transformed and written in terms of the variables m3 and the x-component of m2. |
(C4x)
(C4y)
(C4z)
| The fourth Maxwell equation (a vector equation) as transformed and written in terms of the variables m1 and m4. |
| Fig. 18.2. Maxwell's equations as transformed by the above work, using the Lorentz transforms and written in terms of the variables defined in Fig. 18.1a . | |
We need to solve the above equations for the variables m1, m2x, m2y, etc:
| Inspecting the equations, we see that four of the variables are equal to zero, i.e. (C2y), (C2z), (C4y), and (C4z). Thus ⇒ | m2y = m2z = m4y = m4z = 0 |
|
Multiplying (C1) by V and subtracting it from (C4x) yields
| m4x = 0 . |
| Substituting m4x = 0 into (C1) yields ⇒ | m1 = 0 . |
|
Similarly, we can multiply (C2x) by V and add this to (C3) to yield: | m3 = 0. |
| Inserting m3 = 0 into (C2x) gives ⇒ | m2x = 0 . |
| Fig. 18.3. Solving for m1, m2x, m2y, etc. | |
In summary, all eight of the the variables m1, m2x, m2y, ... , m4z are zero. Using the definitions of these variables as listed above in Fig. 18.1a gives:
|
|
|
|
| Fig. 18.4. Final result of the above work to transform Maxwell's equations using the Lorentz transforms. This shows that in the moving reference frame the laws governing electric and magnetic fields appear to be the same as they were in the stationary reference frame. | |||
Thus, we have successfully shown that the Lorentz transforms when operating on Maxwell's equations, produce the same equations in the new reference frame.
Most text books would do this derivation much more efficiently using more advanced methods, briefly mentioned in Chapter 14. We have presented here this vector algebra derivation as an alternative, in part to illustrate that most physics can be derived in a number of ways and we can learn from each way.
