| All postings by author | previous: 3.20 Wave properties for transmission lines | up: Contents | next: 3.22 Comparison of series and parallel LRC resonant circuits |
3.21 Reflection and absorption coefficients for transmission lines with loads
Keywords: transmission line, reflection coefficient, transmission coefficient
Topics covered in this posting
- One of the most important concepts in the topic of transmission lines is that of how waves on the transmission line interact with a complex load at the end of the transmission line.
- In this posting we derive the basic reflection and "transmission" coefficients for such waves.
- We plot these coefficients in a variety of ways.
- We also derive an expression for the power reflection and absorption coefficients.
- We discuss the complications of the power reflection coefficient.
Contents of this posting
- Basic derivation
- Graphs of complex reflection and transmission coefficients
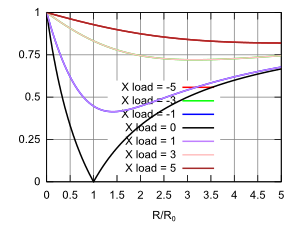
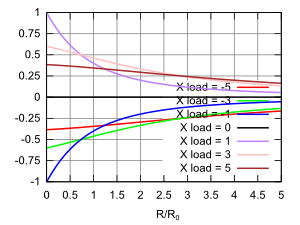
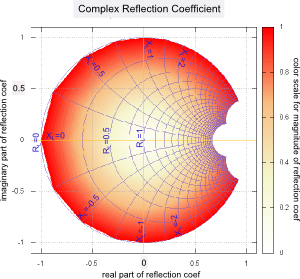
- Figs. 4 and 5 - real and imaginary parts of reflection coef
- Figs. 6 and 7 - magnitude and phase of reflection coef
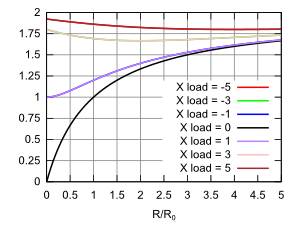
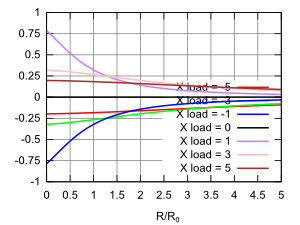
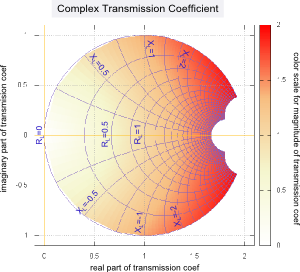
- Figs. 8 and 9 - real and imaginary parts of transmission coef
- Figs. 10 and 11 - magnitude and phase of transmission coef
- Figs. 12 and 13 - complex mapping of reflection and transmission coefs
- Power absorbed by the load impedance
- Error in the second equation for the power reflection coefficient
| 1. Basic derivation |
|---|

In Fig. 1 we see the setup. The incident waves are propagating in from the left, they hit the terminating impedance ZL and are partially reflected. The complex voltage and current amplitudes of the incident wave are V+ and I+ respectively. Those of the reflected wave are V− and I− respectively. The total complex voltage and total current amplitudes due to both incident and reflected waves combined across and through the terminating impedance are VZ and IZ respectively. The above parameters are inter-related by the characteristic impedance of the transmission line and the terminating impedance. The three pertinent equations are: where the minus sign in the middle equation reflects the fact that this wave is propagating in the negative direction and the current associated with the wave is therefore also in the negative direction. These can be rearranged into the forms: The additional equations we need are based on the fact that the voltage VZ and current IZ at the terminating impedance are the sum of the voltages and currents in the incident and reflected waves at the site of the terminating impedance: 
where in the last equation we substituted relationships from (2). Substituting IZ from (2) into the second equation of (3) and using the first equation of (3), the second equation from (3) becomes: Simple manipulations of (4) yield: Equation (5) yields the amplitude reflection coefficient which is the fraction of the incident wave amplitude that is reflected from the load impedance. If either ZL or Z0 are complex, the reflection coefficient (from (5) ) will in general be complex, meaning that there will be a phase shift (other than 180 degrees) in the reflected wave. We can also solve the above equations for the fraction of the incident amplitude that is actually impressed on the load impedance. This is called the amplitude transmission coefficient and equals VZ/V+ . The name makes more sense when the "load" is actually another transmission line with a different characteristic impedance than the one the incident wave is transmitted on as shown in Fig. 2. This coefficient then gives the fraction of the incident amplitude that makes it onto this second transmission line, through the change in characteristic impedance. ZL in (5) and (6) is set equal to the characteristic impedance of this second transmission line.
A careful student might note that the first several steps of (6) show that the amplitude difference between the reflection and transmission coefficients is equal to 1: 
Fig. 3 above shows the reflection and transmission coefficients for real loads on a lossless (with real characteristic impedance) transmission line. Below we graph the real and imaginary parts of the complex reflection and transmission coefficients resulting from complex load impedances in several different ways. |
| 2. Various graphs of the reflection and transmission coefficients | ||||||
|---|---|---|---|---|---|---|
The above graphs and charts assume that the load impedance will involve a positive real part (the resistance R ) and a positive or negative imaginary part (the reactance X ). This is the case for all passive loads whether simple or resonant. For active gain elements these constraints are often not valid. | ||||||
| 3. Power absorbed by the load impedance |
|---|

We can solve for the fraction of incident power absorbed by the load:
where V * is the complex conjugate of the phasor V. See an earlier posting or wiki for a discussion of calculating average power with phasors. In the final step of (8) we have used the fact that any phasor multiplied by its own complex conjugate equals its magnitude squared which is real and can be taken through the Re( ) operator. The first factor on the right side of the equation is just the magnitude of the transmission coefficient in (6) squared. The numerator and denominator can be simplified by using the trick: to yield:
where RL is the real part of the load impedance ZL and R0 is the real part of the characteristic impedance of the transmission line Z0. If Z0 is real (lossless transmission line approximation), then this equation becomes: Fig. 14 below graphs the absorbed power fraction as per Equation (10) as a function of the real part of the load impedance for various values of the imaginary part of the load impedance. Both parts of the load impedance have be divided by the characteristic impedance, which we have assumed to be totally real (a lossless transmission line). We see from the graph that the absorbed power fraction becomes 1.0 only if the imaginary part of the load impedance is zero and the real part equals 1.0 . This is the condition of a load matched to the transmission line and allows all the power in the incident wave to be absorbed by the load. The black curve plots Equation (11), i.e. the condition of the load impedance being real. Fig. 15 is a color mapping of Equation (10) on the complex plane. The axes are the real and imaginary parts of the load impedance. The fraction of power reflected by the load is called the power reflection coefficient. Because of conservation of energy, it is simply one minus the fraction of absorbed power: Another approach to this is to realize that the reflected wave travels on the same transmission line as the incident wave so that we would expect the power reflection coefficient to be the magnitude of the amplitude reflection coefficient squared.

It turns out to be more complicated that (13) implies. Equation (13) is only valid if the characteristic impedance Z0 (see Eqn. (17) of the previous posting) of the transmission line is real. This means (13) is valid only if either we have no (or small) attenuation in the transmission line OR R1 and G1 of the transmission line are balanced to make a distortionless transmission line and G1/C1 = R1/L1 (also called the Heaviside condition). A little algebra will confirm that Eqns. (12) and (13) are not equal unless Z0 is real. Equation (13) is often given in text books because, in practice, most transmission lines are very low loss and often constructed as to be distortionless as well. |
| All postings by author | previous: 3.20 Wave properties for transmission lines | up: Contents | next: 3.22 Comparison of series and parallel LRC resonant circuits |













 . (6)
. (6) . (7)
. (7)



 , (8)
, (8)
 , (10)
, (10)


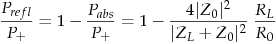
 . (13)
. (13)

 , (15)
, (15)