4. Inverting the Lorentz transforms
We need to use inverse Lorentz transforms in several of the derivations in the coming chapters, so we derive these here. The Lorentz transforms from the previous chapter are:
(4.1a)
|
(4.1b)
|
(4.1c)
|
(4.1d)
|
where
.
These transforms give the primed or moving coordinates as functions of the unprimed or stationary coordinates. We will invert these to give the stationary coordinates as functions of the moving coordinates.
Inverting y and z transforms:
The y and z coordinates, (4.1b) and (4.1c), are trivial:y' = y inverts to give y = y' and
z' = z inverts to give z = z' .
Inverting x and t transforms:
The transforms for x and t are intertwined and must be handled together. We repeat the original x and t transforms:
x' = γ (x − Vt) (4.2a)
t' = γ (t − Vx/c2) (4.2b)
We solve (4.2a) for x:
x = x'/γ + Vt (4.3)
and substitute this into (4.2b):
. (4.4)
Multiplying (4.4) by γ yields:
.
This can be solved for t:
. (4.5)
Substituting (4.5) into (4.3) yields:
. (4.6)
The factor in parenthesis in (4.6) can be reduced as follows:
.
Using this in (4.6) gives:
. (4.7)
Summary
| Lorentz transforms | Inverse Lorentz transforms |
|---|---|
| x' = γ(x − V t) (4.8a) | x = γ(x' + V t') (4.9a) |
| y' = y (4.8b) | y = y' (4.9b) |
| z' = z (4.8c) | z = z' (4.9c) |
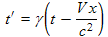(4.8d)
|
(4.9d)
|
Equations (4.9a) through (4.9d) are the inverse Lorentz transforms. They give the stationary (unprimed) x and t coordinates in terms of the moving coordinates (the primed ones). They are also interesting because except for the minus signs in front of the second terms in each equation, they are identical to the original Lorentz transforms, Equations (4.8a) through (4.8d). They can be had from the original transforms by simply substituting −V in place of V. It means that to the moving reference frame, except for the stationary frame appearing to be moving in the opposite direction, it has the same length contraction and time dilation that people in the stationary frame see when looking at the moving frame.
