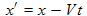| all topics by author | introduction to relativity | contents of mathematics of relativity | previous: wave equation from Maxwell's equations | next: inverting the Lorentz transforms |
3. Invariance of the electromagnetic wave equation to Lorentz transforms
In this chapter, we show that the Lorentz transformations preserve the form of the wave equation, and that the older Galilean transformations do not.
To repeat what we stated in the last posting, the wave equation is of the form:
, (3.1)
where the ψ can be replaced by many different variables, depending on the type of wave involved. This equation is used in many areas of physics, wherever simple wave motion occurs.
Using Galilean transforms on the wave equation
We start with the Galilean transforms. These are listed below. They essentially say that in a uniformly moving reference frame, all is the same, except for in the x direction (the direction of motion of the moving frame). The x coordinate is offset by an increasingly negative value which represents the motion of the moving frame.
| 
|
| 
|
| Fig. 3.1. Table of Galilean transforms. These are the transforms used to change to the coordinates of a uniformly moving reference frame moving at a speed V in the positive x direction. These are valid for speeds that are considerably less than the speed of light, and are thus valid for most everyday experiences. An example might be to change from a ground based coordinate system to a coordinate system aboard (or fixed to) a moving train, moving boat, or airplane. | |
We now use the above Galilean transforms to convert (3.1) from the x and t variables into those of the moving reference frame, x' and t'. We use the chain rule for partial derivatives. You may wonder if we should be transforming ψ also. First of all, we, as yet, don't have such a transformation in this discussion and don't know exactly what we are representing by ψ (we want to keep it general). Secondly, we only are interested in transforming the operator part of the equation, not the variable to which this operator is applied. If we show that this operator is the same, then the transformed equation will have the same solutions and the laws of physics (the waves in this case) will be same in the transformed reference frame. The "laws" are represented by the operator part of the equation.
So we start applying the Galilean transforms to the wave equation, i.e. equation (3.1).
|
|
|
|
|
|
| Fig. 3.2. Galilean transformations applied to the wave equation. |
We see the result in the last line of the above table. This is not the wave equation (at least not the simple wave equation), nor can it be converted into the wave equation by any allowable easy change. The difference represents the fact that in a Galilean world, waves travel at a certain velocity relative to a given fixed reference frame, the reference frame moving along with the wave media. In a second reference frame moving relative to the wave media, the wave equation will not be the standard simple form, and will reflect the fact that in this reference frame the media is moving. An example of this is the propagation of sound on a windy day. A stationary person will not be at rest relative to the wave media (the moving air) and therefore sound will appear to travel faster in some directions and slower in others.
Using Lorentz transforms on the wave equation
In 1887 Hendrik Lorentz came up with a set of space transformations that he claimed would be identical to Galilean transformations at low speed, but would allow Maxwell's equations to keep their same form upon transform. This was to be useful for explaining the experimental determination by Michelson and Morley that the speed of light is constant. In this section, we repeat the transformation process that we did above, but here we use Mr. Lorentz's transforms in place of the Galilean transformations.
We start by listing the Lorentz transformations.
|
|
|
|
where
| |
| Fig. 3.3. Table of Lorentz transforms. | |
Next we use these transformations to transform the wave equation (3.1) written in terms of the x and t coordinates into an equation written in terms of the x' and t' coordinates. We use the chain rule, as we did above for the Galilean transformation.
|
|
|
|
|
|
| Fig. 3.4. Lorentz transformations applied to the wave equation. |
We have used the following fact to cancel terms in the next to last line above:
.
The last line is just the normal simple wave equation written in terms of the primed coordinates, those of the moving reference frame.
We can reverse the above logic to show that if the wave equation is to stay the same (because of the Michelson-Morley result), then the Lorentz transforms must be the correct transformations to be used in changing between initial reference frames.
Einstein concluded from this that the Lorentz transforms therefore indicate how time and space must change in a high speed reference frame. Lorentz concluded that these transforms indicated how the apparent time and space must change.
Conclusions
1. The above derivations shows that the operator part of the wave equation is preserved by Lorentz transformations, but not by Galilean transformations.
2. This means that if the Lorentz transforms are valid then the same electromagnetic waves will occur in all inertial reference frames and that these waves travel at the same speed as determined by the coefficient of the time derivative term.
3. Furthermore, because the wave equations are so tightly coupled to Maxwell's equations (as shown in the previous chapter), this means that Maxwell's equations will hold in all inertial reference frames. We have not addressed the source side of the wave equations which contain the charge density and current density. We shall see in future chapters that the charge and current densities are changed by changing the reference frames; however, this does not affect our conclusion that Maxwell's equations stay the same in all inertia reference frames. Instead, the values of the charge and current density must change.
Einstein interpreted the Lorentz transformations as meaning that time and space were altered by high speed motion, while Lorentz held that these transformations were more mathematical in nature, allowing us to understand what the warping of our physical lengths and temporal events would do to our perception of the time and space. For more on their disagreement, see my introduction to relativity.
| all topics by author | introduction to relativity | contents of mathematics of relativity | previous: wave equation from Maxwell's equations | next: inverting the Lorentz transforms |
