There are all sorts of resonances around us, in the world, in our culture, and in our technology. A tidal resonance causes the 55 foot tides in the Bay of Fundy. Mechanical and acoustical resonances and their control are at the center of practically every musical instrument that ever existed. Even our voices and speech are based on controlling the resonances in our throat and mouth. Technology is also a heavy user of resonance. All clocks, radios, televisions, and gps navigating systems use electronic resonators at their very core. Doctors use magnetic resonance imaging or MRI to sense the resonances in atomic nuclei to map the insides of their patients. In spite of the great diversity of resonators, they all share many common properties. In this blog, we will delve into their various aspects. It is hoped that this will serve both the students and professionals who would like to understand more about resonators. I hope all will enjoy the animations.

For a list of all topics discussed, scroll down to the very bottom of the blog, or click here.

Origins of Newton's laws of motion

Non-mathematical introduction to relativity

Three types of waves: traveling waves, standing waves and rotating waves new

History of mechanical clocks with animations
Understanding a mechanical clock with animations
includes pendulum, balance wheel, and quartz clocks

Water waves, Fourier analysis


Thursday, July 7, 2011

Deriving the electromagnetic wave equation from Maxwell's equations and the reverse


all topics by author introduction to relativity previous: contents of mathematics of relativity next: invariance of the electromagnetic wave equation to Lorentz transforms

illustration of Maxwell, Einstein and a electromagnetic wave

We start off deriving the wave equation from Maxwell's equations. Maxwell's equations in a vacuum (i.e. not inside a material, but with charges and currents present) are:

(2.1a) 2nd Maxwell equation (2.1b)
3rd Maxwell equation (2.1c) 4th Maxwell equation (2.1d)

Fig. 2.1. Maxwell's equation for electromagnetic fields in a vacuum (meaning that there are no materials present that affect electric or magnetic fields such as ceramic or iron).

These equations, as shown, are written in vector calculus notation as is commonly taught in a junior level electromagnetic fields course in physics or electrical engineering. An online references of the appropriate level but rather old in style is MIT open courseware. Several of the better textbooks on this subject at an appropriate level and newer in style that the author is familar with listed below. The exact edition of each is not so important.


To derive the wave equation, it is useful to convert the above equations in E and B fields into equations involving their associated potentials, φ the electric potential and A the magnetic vector potential. These two potentials are defined by the relations:

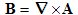
definition of the vector potential, A (2.2a) definition of the scalar potential (2.2b)

It turns out that (2.2a) does not completely define A, that we are free to arbitrarily define the divergence of A without affecting B through (2.2a). Conventionally this is done by setting a "gauge" to be the Lorentz gauge, given by the equation:

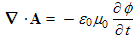
the Lorentz guage (2.3)

One of the advantages of using the potentials φ and A is that two of Maxwell's equations are automatically satisfied, (2.1b) and (2.1c), since the divergence of the curl, ∇·(∇×A), and the curl of the gradient, ∇×∇φ, of any well behaved vector or scalar fields are both identically zero:

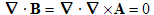
alternate form of 2nd Maxwell equation (2.4a)
alternate form of 3rd Maxwell equation (2.4b)

We also used the fact that we are free to interchange the order in which the time and space partial derivatives are performed.

Now we use (2.2a), (2.2b), and (2.3) to write the two remaining Maxwell equations, (2.1a) and (2.1d), in terms of φ and A.

The first Maxwell equation becomes:

alternate form of 1st Maxwell equation     or (2.5a)
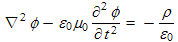
scalar potential - inhomogeneous wave equation (2.5b)

The fourth Maxwell equation becomes:

alternate form of 4th Maxwell equation     or (2.6a)
alternate form of 4th Maxwell equation      and (2.6b)
vector potential - inhomogeneous wave equation (2.6c)

The boxed equations, (2.5b) and (2.6c), are inhomogeneous wave equations, wave equations with sources (i.e. charge density ρ or current density J) on the right sides. In regions of space containing no charges or currents (i.e. ρ = 0 and J = 0), the right sides of these equations are zero and the equations are known as the homogeneous wave equations. They both support wave propagation at the velocity equal to one over the square root of the multiplier of the ∂2/∂t2  term, i.e. at a velocity given by 1/√μ0ε0 . This happens to equal the known speed of light. Maxwell, in the early 1860's, derived these equations and made the connection that light must be the electromagnetic waves that these equations describe.

Discussion of a one dimensional homogeneous wave equation

To give the reader a taste of wave equations, we briefly discuss the simplest wave equation, the one dimensional homogeneous wave equation. The following equation describes propagation of a plane wave in the x direction:

one dimensional wave equation (2.7)

where α is a constant of the equation and ψ is the variable of the wave. If this were an equation describing sound waves, ψ would be the acoustical pressure, i.e. the small pressure oscillations associated with the passage of a sound wave.

Suppose we take a snapshot of the wave at a particular time, say at t = 0  and we find a function that describes the wave at this time. It can be any arbitrary function. Call this function f(x) .

It is easy to show that if we replace the x in the function by u = x − vt  that this new function satisfies (2.7) and that a graph of this new function will appear to shift to the right with a velocity, v, given by v = 1/√α. For example, suppose a snapshot of a possible wave is given by the function ψ(x) = sin kx at t = 0 . Then the function ψ(u) = sin k(x−vt) satisfies (2.7) and is a possible description of the wave as a function of time.

We show that f(u) satisfies (2.7) by substituting f(u) into (2.7) and using the chain rule for derivates.

We start out by calculating the first term in (2.7):

Then the second term:

Putting the two terms together, we have a total of zero thus showing that a function of our u is indeed a solution of the wave equation (2.7):

We could alternately have used u = x + vt  (with a plus sign) with the same result or any linear combination of the two solutions. These solutions by d'Alembert (1717-1783) have the property of shifting the function f to the right (with the minus sign) or to the left (with the plus sign) at velocity v.

Equations (2.5b) and (2.6c) are similar to (2.7) but instead of being applicable to a one dimensional wave traveling in the x direction, these govern complicated waves traveling in any direction in three dimensional space. Equation (2.5b) involves wave-related oscillations in a scalar, the electric potential φ, while (2.6c) involves similar oscillations of a vector field, the magnetic vector potential A.

A physicist with the mathematical prowess of James Clerk Maxwell (1831-1879) would immediately recognize (2.5b) and (2.6c) as wave equations, and that they predict the existence of an electromagnetic wave with a velocity equal to 1/√ε0μ0 . Both of the constants ε0 and μ0 had been previously determined by measuring the electric and magnetic interactions of charged objects and current-carrying wires in the laboratory. When Maxwell calculated the velocity of these newly found waves, he got a value very close to the known speed of light, indicating to him that he had just shown that light was a wave of electromagnetic fields. This further settled a long standing debate as to the exact composition of light that had been raging for centuries among the giants of physics including Aristotle (384-322 BC), Newton (1643-1727), Huygens(1629-1695), and Young(1773-1829).


Derivation of Maxwell's equations from the wave equations

Above we derived the wave equations from Maxwell's equation. In this section we do the reverse, showing that Maxwell's equations can be derived from the wave equations. Basically it is just a process of retracing our early steps, in reverse order.

First off, two of Maxwell's equations (the second and third ones) automatically hold, from the definitions of φ and A as shown in (2.4a) and (2.4b) above.

The two inhomogeneous wave equations from above are:

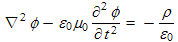
scalar potential - inhomogeneous wave equation (2.8a) vector potential - inhomogeneous wave equation (2.8b)

To derive the first Maxwell equation, we start with (2.8a), and reverse the steps in (2.5a). We use the Lorentz gauge, (2.3), to replace the time derivative of φ with a space derivative of A. This makes the second term in (2.8a) become:

(2.9)

Substituting this into the left side of (2.8a) gives:

(2.10)
Equating this with the right side of (2.8a) and multiplying through by −1, we have the first Maxwell equation (2.1a):
1st Maxwell equation   (2.11)

To derive the fourth Maxwell equation, we start with the vector wave equation (2.8b) and reverse the steps in (2.6b) and (2.6a). First we add and subtract the quantity ∇(∇·A) to the left side of (2.8b):

(2.12)

We then make use of a vector calculus identity for the first two terms and make use of the Lorentz gauge (2.3) for the third term:

(2.13)

Finally we use (2.2b) to combine the last two terms of (2.13) to get:

4th Maxwell equation (with minus sign)   (2.14)

We have also set the result equal to the right hand side of the vector wave equation (2.8b). This is obviously just the negative of the fourth Maxwell equation (2.1d) shown above.

Conclusion

We have shown with the above math that the Maxwell equations can be used to derive wave equations of the electric and magnetic vector potentials, φ and A. We have also shown the reverse, that the inhomogeneous electromagnetic wave equations can be used to derived the Maxwell equations.


all topics by author introduction to relativity previous: contents of mathematics of relativity next: invariance of the electromagnetic wave equation to Lorentz transforms

Posted by P. Ceperley at 10:53 AM