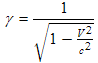There are all sorts of resonances around us, in the world, in our culture, and in our technology. A tidal resonance causes the 55 foot tides in the Bay of Fundy. Mechanical and acoustical resonances and their control are at the center of practically every musical instrument that ever existed. Even our voices and speech are based on controlling the resonances in our throat and mouth. Technology is also a heavy user of resonance. All clocks, radios, televisions, and gps navigating systems use electronic resonators at their very core. Doctors use magnetic resonance imaging or MRI to sense the resonances in atomic nuclei to map the insides of their patients. In spite of the great diversity of resonators, they all share many common properties. In this blog, we will delve into their various aspects. It is hoped that this will serve both the students and professionals who would like to understand more about resonators. I hope all will enjoy the animations.

For a list of all topics discussed, scroll down to the very bottom of the blog, or click here.

Origins of Newton's laws of motion

Non-mathematical introduction to relativity

Three types of waves: traveling waves, standing waves and rotating waves new

History of mechanical clocks with animations
Understanding a mechanical clock with animations
includes pendulum, balance wheel, and quartz clocks

Water waves, Fourier analysis


Saturday, July 9, 2011

Derivation of length contraction and time dilation from Lorentz transformations

all topics by author introduction to relativity contents of mathematics of relativity previous: inverting the Lorentz transforms next: constant velocity of light from the Lorentz transforms

In this chapter we start with the Lorentz transformations and show that they can be used to derive length contraction and time dilation.

Derivation of length contraction:

Length contraction refers to a moving object appearing to look shorter when viewed in the stationary reference frame. (Lorentz would say that it really does become structurally shorter, while Einstein would say the metric has changed making it shorter.) We consider measuring the length of our object as taking measurements of the positions of the two ends x1 and x2 at the same time in the stationary reference frame. That is to say t1 = t2.

We need a transform that would let us use this fact, as well as relating x1 and x2 to x1' and x2'. That is to say we need a transform that involves t1, t2, x1, x2, x1', and x2'. Looking through the list of Lorentz transforms and inverse Lorentz transforms, we decide that the first Lorentz transform involves these variables:

      x' = γ (x − Vt)      (5.1)

where    relativistic gamma factor       (5.2)

Applying this transform to the measurement of the two ends of the object, we have:

      x1' = γ (x1 − Vt1)      (5.3)

      x2' = γ (x2 − Vt2)      (5.4)

Subtracting the first equation from the second to get the length, we have:

      length' = x2' − x1' = γ [(x2 − x1) − V(t2 − t1)] = γ (x2 − x1) = γ × length      (5.5)

where we have used the fact that t1 = t2 makes the time difference factor zero. Inverting the equation we get:

     length = length'/γ    .      (5.6)

Since γ is always equal to or greater than 1, we see that the length in the stationary frame (the unprimed frame) will be equal to or smaller than the length in the moving frame (the primed frame, inside of which the object appears stationary). The faster the object is moving, the larger γ will be and the greater the effect of length contraction will be.

Derivation of time dilation:

Time dilation refers to the time duration of a physical process in a moving object appearing to take longer when viewed from the stationary reference frame (which the object is moving relative to). Similar to the derivation of length contraction, we consider measuring the time duration of a process in the object which is stationary in the moving frame, but we wish to transform the starting and ending times of the process to the stationary frame. Since the object is stationary in the moving frame, x1' = x2'  where x1' and x2' are respectively the starting and ending positions of the object in the moving reference frame.

We need a transform that will let us use the fact that x1' = x2' and also relates t1'and t2' to t1 and t2. That is, we need the Lorentz transform that involves x1', x2', t1', t2', t1, and t2. Looking through all the Lorentz transforms and inverse Lorentz transforms, we decide that the last inverse Lorentz transform involves these variables:

      t = γ (t' + Vx'/c2)    .     (5.7)

Applying this transform to the start and finish times of our process, we have:

      t1 = γ (t'1 + Vx1'/c2)    .      (5.8)

      t2 = γ (t'2 + Vx2'/c2)    .      (5.9)

Subtracting the first equation from the second to get the time duration of the process, we have:

      Δt =  t2 − t1 = γ [t2' − t1' + (x2' − x1')V/c2] = γ (t2' − t1') = γ Δt'    .      (5.10)

Or in summary (equating the first and last):

   Δt = γ Δt'    .   (5.11)

Since γ is always equal to or greater than 1, we see that the time duration Δt of a moving process observed in the stationary frame is equal to or larger than the time duration, Δt', observed in the moving frame, moving along with the process. The faster the object is moving, the larger γ will be and the greater the effect of time dilation will be. Another way to say this is to say that moving processes seem to slow down when viewed from the stationary reference frame.

all topics by author introduction to relativity contents of mathematics of relativity previous: inverting the Lorentz transforms next: constant velocity of light from the Lorentz transforms

Posted by P. Ceperley at 9:29 AM