Resonances, waves and fields: Derivation of the Lorentz transforms starting with length contraction and time dilation

Monday, July 11, 2011

8. Derivation of the Lorentz transforms starting with length contraction and time dilation

We begin by explaining the Galilean relativity motion transforms and then go on to derive the Lorentz transforms, both shown in Fig. 8.1 below. Both sets of transforms assume that the unprimed reference frame (with coordinates x, y, z, and t) is stationary and the primed frame (coordinates x', y', z', and t') is moving in the x-direction at constant velocity V.

Galilean transforms			Lorentz transforms


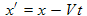
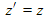
			where
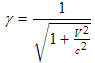
Fig. 8.1. Table of Galilean and Lorentz transforms.

The length contraction and time dilation formulas are:

, (8.1) and

Δt = γ Δt' , (8.2)

where the relativistic factor γ is given by:

(8.3)

The x transform:

The first Galilean transform is easy to understand. It says that a stationary point in the stationary reference frame having x-coordinate value of x will appear to be sliding to the left from the point of view of someone in the moving frame. In that reference frame, the point will appear to shift an amount −Vt, i.e. its x' coordinate value will be given by the initial x value plus this shifting amount:

x' = x − Vt (8.4) .

In the relativistic case we need to account for the length contraction in the x-direction. That is, the x' scale will be shrunk and the same value in the x coordinates will translate to larger x' values because of this shrinking. The relativistic factor

(8.5)

is needed here to multiply the x' coordinate in (8.4) and complete the transform:

x' = γ (x − Vt) (8.6) .

The y and z transforms:

The y and z transformations are really not transformations at all, because there is no relative motion in these directions and also no length contraction in these directions. So in both the Galilean and relativistic cases:

y' = y and z' = z (8.7) .

The time transform:

In the Galilean case, the time transform is trivial, i.e. there is no transform and t' = t.

On the other hand, in the relativistic case, deriving the time transformation takes some work. The first term in the Lorentz time transform is easy: it is just the time dilation factor γ applied to the original time t.

t' = γ t (8.8) (incomplete!).

So what about the extra −Vx/c² term in the last Lorentz transform equation in Fig. 8.1? It might be called the synchronization term. It insures that time at the various points in the moving frame will appear to be synchronized to a person in that frame, as you might expect.

We would expect our time to be synchronization, that time did not seem to vary with the coordinate x . However we saw in the previous chapter that when we change reference frame, previously simultaneous events are no longer simultaneous, if they have different x values.

In the previous chapter, we found that two events that are simultaneous in the stationary frame will have a time difference between them of Δt = γΔxV/c² (see Equation (7.11) ). If we wish to correct for this time difference we need to subtract it from t in Equation (8.8):

t' = γ (t − xV/c²) . (8.9)

Equation (8.9) is the time part of the Lorentz transformations. Without this last term, a person on a moving frame would sense that clocks located in different x-positions in his frame would not be synchronized, assuming they were synchronized the stationary frame.

Simultaneity in high speed reference frames:

Because of the last term in (8.15), simultaneity is not longer a simple issue at relativistic speeds, i.e. at speeds close to that of light. At low speeds, if two events occur at the same time, i.e. simultaneously, then they occur at the same time in all moving reference frames, even if the two events are at two different locations. Thus if lightning strikes two different trees at the same time as witnessed by a stationary observer, then an observer flying at low speeds overhead will also see the two strikes occurring at the same time assuming the observers are about the same distance from the two strikes. On the other hand, if an airborn observer is traveling at relativistic speeds, even if he is equidistant from the two strikes (that are simultaneous in a stationary frame), the two strikes will not appear occur at the same time to this flying observer.

The last term in (8.15), i.e. the synchronization term, means that for high speed motion, the time in a high speed moving reference frame depends of both the x position and on the velocity of the frame, V. Thus, two events occurring at the same in the stationary frame, so that t₁ = t₂, will not have the same time in the moving frame if they have different x coordinates which make the last terms in (8.15) differ and in turn make t₁' ≠ t₂'. In general, for relativistic speeds, simultaneity of two events that have different x coordinates, only holds in a particular reference frame.