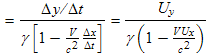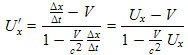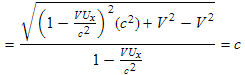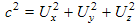| all topics by author | introduction to relativity | contents of mathematics of relativity | previous: Lorentz transforms from length contraction and time dilation | next: relativistic mass |
9. Transforming velocities
The idea behind this section can be a little hard to wrap your mind around, because it involves two different velocities at the same time. In the stuff above, we have worried about just one velocity. In the previous chapters in one reference frame, the object in question was moving, and in the other frame, the frame moving with the object, the object is at rest or stationary. Now we are considering the situation where the object is moving with respect to both our reference frame, moving with respect to the "stationary" frame and moving with respect to the "moving" frame. The question that we address here is: if the object is moving at velocity U with respect to the stationary frame, then how fast will it be traveling with respect to our moving reference frame, moving with velocity V in the x direction?
We will consider two cases: when the object is moving perpendicular to the motion of the moving reference frame and secondly, when it is moving parallel to the motion of the moving reference frame. You can use these two transforms for transforming the perpendicular and parallel components of a velocity at any arbitrary angle. You can read more about the general case here.
Velocity perpendicular to the motion of the reference frame
Here we see how an object moving perpendicular to the direction of the motion of the reference frame changes its y' coordinate (in the moving reference frame), i.e. Δy' for a given time period, Δt'. We assume that the object starts at y' = y1' and ends the time period with y' = y2'. The beginning and ending times are t' = t1' and t' = t2' , respectively. We use the Lorentz transforms to convert these quantities to the stationary reference frame (the unprimed frame).
. (9.1)
Above we've used the fact that the motion is perpendicular to mean that Δx is equal to zero. The final result shows that the y motion is reduced by the γ factor, which you might attribute to time dilation (time appears to be slowed down in another reference frame).
Velocity parallel to the motion of the reference frame
In this section we repeat the calculation for a velocity parallel to the motion of the moving reference frame, i.e. in the x direction. The calculations are made a little more complicated by the fact that the x transformation is more involved than the y transformation, and also by the fact that we can't declare the Δx term to be zero as we did above. In the end we have a little more complicated expression than we did in the previous derivation.
. (9.2)
We continue by dividing both the numerator and denominator by Δt :
. (9.3)
Summary of velocity transform
| Table 9.1. Transformation of velocities | |
|---|---|
| Component of velocity parallel to the relative motion of the reference frame |
(9.4a)
|
| Component of velocity perpendicular to the relative motion of the reference frame |
(9.4b)
|
| Other component of velocity perpendicular to the relative motion of the reference frame |
(9.4c)
|
Transforming the speed of light in an arbitrary direction
If we change from one reference frame to another, we would expect the direction of any light pulse to change, however the speed of light should stay constant. We next check this out using the above equations:
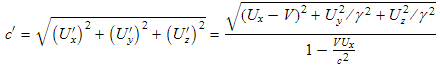
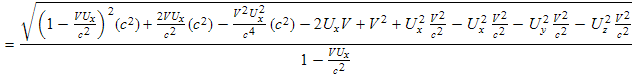
In the last step we made use of the fact that the magnitude of U equals the speed of light:
.
The above algebra shows that the velocity transforms (9.1) and (9.3) are consistent with the speed of light being invariant, i.e. anything traveling at the speed of light in any direction will be traveling at the speed of light in a Lorentz transformed frame.
| all topics by author | introduction to relativity | contents of mathematics of relativity | previous: Lorentz transforms from length contraction and time dilation | next: relativistic mass |
