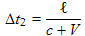| This posting includes flash animations showing the physics discussed. Most computers have a flash player already installed, but if yours does not, download the free Adobe flash player here. |
7. Length contraction and time dilation from a constant speed of light
This chapter follows Einstein's logic. Einstein starts with the assumption that physics will be the same in all the uniformly moving reference frames (also called inertial reference frames) and also with the corollary that the speed of light is constant in all these reference frames. From these concepts he derives the laws of high speed motion. This particular chapter uses these two concepts to derive length contraction and time dilation, as well as constancy of length perpendicular to motion and changes in simultaneity. From these, a person can derive the Lorentz transforms (see Chapter 8) and the many other equations of special relativity (some of which are derived in Chapters 9 - 18 of this posting).
A novice to the concepts of relativity might find these derivations a bit strange. How can little timing differences in light beams mean that time and distance is warped? Well, a constant speed of light is truly odd and Einstein's thought experiments are just sticking our faces into the logical consequences of the speed of light really being the same for all uniformly moving reference frames. In order that simple experiments concerning light beams show that light is moving at the same speed to both a stationary and a moving observer, we end up concluding strange things: that either space and time warp, as Einstein held, or that objects distort and slow their internal processes, as Lorentz held. If you find this chapter confusing and haven't read my earlier blog on understanding special relativity this might be a good time to go back and read it. It explains Einstein's view of these oddities, as well as Lorentz's. Many readers might find Lorentz's view of these oddities more understandable. Both views are mathematically equivalent.
Assumptions and conclusions of this chapter
Assumptions
1. Physics obeys the same rules and equations in all uniformly moving reference frames.
2. Light moves at the same constant value in all uniformly moving reference frames (this is implied by #1 above, i.e. it's a corollary to #1).
Conclusions of this section
1. Lengths perpendicular to the relative motion of the moving reference frame are unchanged by the motion.
2. Temporal processes are slowed in moving objects. This is called time dilation.
3. Lengths in the direction of the relative motion are shrunk by the motion. This is call length contraction.
4. Events at different x coordinates (parallel to the direction of motion) which occur simultaneously in a particular reference frame will not be simultaneous in other reference frames moving relative to the first one in the x direction.
Relativity and reference frames
Relativity is all about high speed motion, i.e. the properties of particles and masses when they are moving at velocities close to the speed of light. The physics of relativity is commonly presented in terms of changing reference frames. This allows the physics of low speed objects to be transformed into the physics for very rapidly moving objects.
Often we speak of two reference frames, one stationary and one moving. The moving reference frame is taken to be moving along with a speeding particle that we happen to be studying, so that to someone in that reference frame the particle would be at rest and its physics well understood. In the stationary frame the particle would be moving. We make transforms that let us adapt the physics in the moving frame (in which the particle is at rest) so that it is valid in the stationary frame (in which the particle is moving at very high speeds).
It is common to designate properties in the two reference frames as primed and unprimed, such as x' and x. We will take the primed frame to be the moving frame, in which the particle is often at rest. The stationary frame will have its properties not primed, i.e. such as x. Note that it is common to call the properties as measured in a reference frame in which a particle is at rest the "proper" properties, such as the "proper length" or "proper mass".
Perpendicular to motion, no change in length
Fig. 7.1a. An animation illustrating the difficulty of measuring the length of a moving object. The viewer can compare the "measured length" when the end positions are determined (or "marked") simultaneously and when they are not. This animation shows the error in failing to mark the two end positions at the same time. Mouse over the animation to start it and mouse off to suspend it. Click on it to restart it, or if it fails to start. |
To "measure" the length of a moving ruler, we first determine the positions of its two ends, both at the same instant in time; then we measure the distance between these positions. It is critical that the positions be determined at the same instant in time, i.e. simultaneously, or the motion of the moving ruler will add an error. The animation in fig. 7.1a illustrates this. Mouse over the animation to start it.
The proof of the lack of perpendicular length change is based on the next animation, Fig. 7.1b. In this figure we see two identical rulers (except for their color), identical when both are brought to rest beside each other, both oriented perpendicular to the relative motion of the reference frames. In this thought experiment, one ruler is made to move along with the moving frame while the other is fixed to the stationary frame. We show one ruler longer just to illustrate that perhaps one ruler's length is changed by the motion. We will end up concluding that this is not true, that in fact they both remain equal in length despite their relative motion.
Fig. 7.1b. An animation illustrating that in the perpendicular direction, lengths are not changed by relative velocity. If they were to be changed by motion, then one of the lengths would be measurably longer than the other in both reference frames (as incorrectly shown in this animation). This would mean that to an observer in one reference frame, motion would seem to shorten a ruler while in the other reference frame motion would appear to lengthen an identical ruler. This difference would violate the first assumption above. The core of the animation is really just the comparing of the rulers' lengths when they pass and seeing that if they differ in length, observers in both reference frames would agree on which ruler was longer. The light pulses resolve a secondary issue, simultaneity. These pulses are shown in red and blue and demonstrate that the upper ends of the rulers pass each other at the same instant in time as the lower ends, as seen in both reference frames, so that we do not have simultaneity issues which were addressed in Fig. 7.1a. Mouse over (or click) the figure to start the animation. Mouse off to suspend it and click on it to restart it. Read the text at the left to further understand it. |
The rulers are positioned so that their centers go past each other. We adjust the coordinate system so the the rulers' centers are on the x axis as shown. At the instant that the rulers go past each other, observers in both reference frames can tell if they are the same length, i.e. if their ends coincide at the instant they pass each other.
Much of the animation is directed towards demonstrating that the two ends of each ruler pass the other ruler at the same instant in time, that there is no time offset between the passing of the upper and lower ends which could confuse the issue of simultaneity as illustrated in Fig. 7.1a. The demonstration of simultaneity is done by emitting light pulses at the instant the rulers pass each other and showing that the upper light pulses (from the upper ends of the rulers) arrive at the centers of the rulers at the same times as do the lower light pulses.
Because the setup is symmetrical around the x axis, the pathlengths the light pulses travel from the top sources are the same as the paths that the bottom pulses travel. This means that the light from the top sources will arrive at the detectors (i.e. centers of the rulers) at the same times as those from the bottom sources. This is true when we are considering light propagating to the stationary ruler's detector or we are considering the moving ruler's detector. Click on Fig. 7.1b to see this in animation. With equal pathlengths, coincident arrival times mean that the top end of the rulers pass over each other at the same time that the bottom ends do, both from the point of view of the moving ruler and from the point of view of the stationary ruler.
To further facilitate the ease of comparing the two lengths, we arrange marking mechanisms at all the ends of the rulers. These put marks on the the opposite ruler's space when the rulers pass by each other. You can see the yellow and blue x's being made in the animation at the instant one ruler passes the other. As was pointed out in the above discussion concerning light pulses, both reference frames agree that the two marks are made at the same time.
The marks and the rulers ends are physical entities that can be examined in either reference frame. It is also true that their relative positions will be the same in either reference frame. We have purposely (and incorrectly) drawn the moving ruler longer than the stationary one so you can understand this point. You can see that after the rulers pass, the marks on either ruler clearly show that the blue (moving) ruler is longer than the yellow (stationary) ruler. (Temporarily mouse off the animation to suspend it part way through so you can examine the markings more easily.)
Two results are possible: either the marks coincide with the other ruler's ends or they don't. If they don't, then one party's ruler appears shorter in both reference frames. In other words: to a stationary observer, the moving blue ruler appears longer and the motion of the blue ruler has increased its length. To an observer moving along with the blue ruler, the yellow ruler (which will appear to be moving relative to this observer) appears shorter: the relative motion of the yellow ruler appears to have shunk the yellow ruler's length. This means that the laws of physics of motion would be different in the two reference frames: in one case motion increased the moving ruler's length, in the other case it shrunk the moving ruler's length. We could use this to determine which reference frame had greater velocity relative to some absolute stationary frame, a concept that Einstein resolutely did not believe and which clearly violates assumption 1 above.
Thus, if we hold our assumptions to be valid, motion cannot result in perpendicular lengths being altered and we are incorrect in drawing our two rulers in Fig. 7.1b as different in length, since they are supposed to be identical when stationary. In conclusion: two rulers with the same proper lengths will stay equal in length when one of them is set into motion relative to the other provided that the rulers are orientated perpendicular to the direction of their relative motion.
Derivation of time dilation
For this section, we use a very special clock which is based on the propagation of light, shown in Fig. 7.2a, appropriate because of the special place light had in Einstein's theory. The nice feature of this clock is that it is particularly easy to understand the effect that relative motion has on it if we keep to our assumption about the constant speed of light. The result will be same as we would get with another clock design based on electromagnetic interactions. This special clock involves a light source that emits a light pulse that travels upwards to a mirror and back down to a detector located right beside the source. At this point another pulse is sent upwards and the process repeats again and again, presumably with a counter to count off these "ticks" of the clock. However, here we will concern ourselves with just one tick of this clock.
Fig. 7.2a. Animation showing time dilation. The illustration shows two of Einstein's light clocks, one stationary (at the far left) and one moving across the screen. The light beams in both clocks travel at the standard speed of light. However, because the diagonal distance that the light has to travel in the moving clock is greater, the clock cycle in that clock takes longer than in the stationary clock, i.e. that clock is slowed down. In the text below we calculate the amount of this slowing. We show the light pulses leaving trails to further highlight the path lengths of the two pulses. At the end of one clock cycle, we freeze the motion to allow you to better study the paths. Mouse over (or click) the figure to start the animation. Mouse off to suspend it and click on it to restart it. Read the text below to understand it. |
Fig. 7.2a animates the two clocks while Fig. 7.2b is a snap shot at one instant of time, highlighting the paths in the animation.
As we have just seen in the previous section, the vertical lengths of the paths will be unaffected by the motion and will equal h, where h is the non-moving height of the clock. The horizontal length of the half path under the diagonal (shown in Fig. 7.2b) is VΔt/2 where V is the speed of the clock and Δt is the time of one "tick" of the moving clock. The diagonal distance is cΔt/2 because the pulse travels at c, the speed of light. Writing out the Pythagorean theorem for this right triangle, we have:

|
Fig. 7.2b. Snapshot of the animation above highlighting the trajectory of the light pulse. We have also labeled the three sides of the right triangle in the above Pythagorean theorem equation. |
Equation (7.1a) can be solved for 2h which we will need in a moment:
We next slip into the moving reference frame. In that reference frame, the clock will be at rest. Also, according to Einstein (and a wealth of experimental evidence) the speed of light will be the same standard value in this reference frame. Thus, in the moving frame, the light pulse will be vertical (or nearly so) as illustrated by the stationary "clock" in the animation, Fig. 7.2a. In this reference frame (the moving reference frame) we use primes on values, so one clock tick in this reference frame will be designated as Δt'.
In one tick, the light travels upwards the height of the clock, then downwards the same distance again, this height h being the same value in both reference frames, as we saw in the section above. Thus we write 2h = cΔt'. Substituting 2h from (7.1b), we have:
This can be solved for Δt:
where γ is defined as:
In summary, assuming that light travels at the same speed in all uniformly moving reference frames, we have shown that the time interval Δt (as measured by our "light clock") will be increased by motion as given by:
Note that γ equals 1 for zero or low velocities (V << c) and becomes larger at higher velocities. It trends to infinity as the velocity, V, approaches c. This means that at low velocities, the time intervals is not affected by the motion and Δt equals Δt'. On the other hand at velocities very near the speed of light, Δt can be much greater than Δt' depending on the speed and the time interval can be greatly lengthened.
So far we have been considering time durations in our experiment shown in Fig. 7.2a, but this result is much more general than that. If we take light to be the essence of all electromagnetic interactions, we can surmise that if the apparent speed to light is really the same for all uniform reference frames, all electromagnetic processes must slow down as per (7.3) and that Δt could refer to the time length of all sorts of physical process inside speeding objects. For example Δt can refer to the length of one cycle of a clock on board an orbiting satellite, or it can refer to the average time it takes for the subatomic particle, the muon, to decay when it is in high speed motion. And indeed, clocks aboard an orbiting satellite do in fact run slow as compared with their counterparts on the ground, consistent with (7.3). Also, muons traveling at great speeds inside a particle accelerator do in fact have longer decay times that those that are stationary, consistent with (7.3).
The slowing of temporal events and physical processes due to speed as per (7.3) is called time dilation and has been experimentally verified many, many times in various ways.
Derivation of length contraction
The approach to this derivation is to calculate the time it takes for a light pulse to travel the length of a moving ruler in the direction of motion. See figure 7.3 for the setup. We correct for the distance the ruler has moved in this time. We then assume that the light pulse traveled at a speed equal to that of light, i.e. c and calculate the length of the ruler based on this.
Fig. 7.3. Experiment to determine the transformation of lengths in changing from a stationary to a moving reference frame. The setup here is basically one of Einstein's "clocks" shown in the previous animation, but here it is tipped on its side so the light pulse travels in the direction of the motion of the whole clock. We have the light pulse leave a trail in the stationary reference frame, so you can better see its path in this frame. Mouse over (or click) the figure to start the animation. Mouse off to suspend it and click on it to restart it. Read the text below to understand it. |
We start by examining the first part of the experiment, the part when the light travels from the source to the mirror. We assume it takes time Δt1 to travel from the source to the mirror. During this time, the ruler has moved a distance:
Δxruler = VΔt1 . (7.4)
During the same time the light pulse has traveled the distance:
d = cΔt1 . (7.5)
This includes the length ℓ of the ruler plus the distance the ruler has moved, i.e.:
d = ℓ + Δxruler . (7.6)
We can substitute (7.4) and (7.5):
This can be solved for Δt1 :
There is a mirror at the far end of the ruler, so that the light is reflected back to the source (and detector). This second part is assumed to take a time Δt2. Now the light pulse is going in the opposite direction as it was before so now in place of (7.6) we get:
d = ℓ − Δxruler , (7.8)
i.e. the ruler's motion reduces the length the light travels. Substituting as before for d and Δxruler (i.e. using (7.4) and (7.5) ) and using Δt2 in place of Δt1, we have:
This can be solved as:
The total time for the light to go from the source to the mirror and back to the source is given by:
 . (7.9)
. (7.9)
Next, we switch into the other reference frame, the moving one, in which the ruler is at rest. Einstein says that the speed of light is the same value, and in this reference frame there is no motion other than that of the light pulse. So we can write Δt' = 2ℓ'/c where Δt' is the time in the moving frame of one clock cycle, and ℓ' is the length of the ruler in this frame. Using the above derived time dilation expression (7.3), this becomes Δt/γ = 2ℓ'/c or Δt = 2γℓ'/c .
Substituting this into the above expression for Δt , i.e. into (7.9), we get 2γℓ'/c = (2γ2ℓ/c) which can be solved for ℓ to yield:
This last expression captures the essence of length contraction, that an extremely rapidly moving object appears shorter in the direction of motion than it is when at rest or moving slowly.
Simultaneity
One of the oddities of relativity is that two events that occur at the same time in one reference frame will not be simultaneous in another reference frame. To understand this, consider the experiment shown in Fig. 7.4. In this experiment we have a moving ruler with a light pulse source in the middle. The light source sends pulses to detectors at the two ends of the ruler. We consider the pulses reaching their respective detectors to be the two spacially separated events in this experiment.
In the frame moving along with the ruler, the two light pulses would reach the two detectors simultaneously, meaning that in this, the moving reference frame, the events are simultaneous. In the stationary frame, in which the ruler is moving, the situation is quite different and the motion will shorten the transit time of the left pulse and lengthen that of the right pulse. Thus, in the stationary frame, the two events are not simultaneous.
We next calculate the error in synchronization (i.e. in simultaneity).
Fig. 7.4. Animation of a gedanken or thought experiment on relativistic simultaneity described above in the text. In this animation, we show the paths of both light pulses to help with the understanding. It may look like the two paths are too different to be real, but if you examine the animation carefully (stopping it when needed) you will see that the difference in the path lengths is purely due to the motion of the detectors. The difference is due to one beam having to catch up to a detector moving away from it while the other beam only has to run into a detector coming towards it. The animated velocity of the ruler is V = 0.7c . Mouse over (or click) the figure to start the animation. Mouse off to suspend it and click on it to restart it. |
The distance that the right light pulse must travel in the stationary frame is given by
where we have applied length contraction (i.e. the 1/γ or Eqn. (7.10) ) to the half ruler length, ℓ'/2, as measured in the moving frame. Also Δt1 is the propagation time (measured in the stationary frame) and VΔt1 is the distance the moving assembly moves in that time. We can solve this equation for Δt1 as:
We repeat this for the left light pulse. The distance this pulse travels is:
which can be solved for the transit time of the left pulse:
The difference in transit times (measured in the stationary frame) for the synchronization pulses to reach the two clocks is:
 .
.
Rewritten, using Δt as the difference in time intervals on the left side of the above equation, we have:

In summary, in the line above we calculate the error in synchronization between two clocks that are synchronized in a moving reference frame. We will use this as one of the terms in the Lorentz transformations.
Summary
| Item | Effect | Equation |
|---|---|---|
| Lengths perpendicular to reference frame motion | No change | Δy = Δy'
Δz = Δz' |
| Lengths parallel to reference frame motion | Length contraction | Δx = Δx'/γ |
| Time intervals | Time dilation | Δt = γΔt' |
| Two simultaneous events separated in the x direction | Change in simultaneity upon change of reference frames | Δt = γΔxV/c2 |