15. Transformation of electric and magnetic fields
Computational strategy
We cannot feel or see electric and magnetic fields. We hypothesize them to account for forces and trajectories of charged particles and currents. Electric and magnetic fields are detected or "felt" with charges and currents. Along these lines, in order to figure out how electric and magnetic fields transform under change in reference frame, we must see how the Lorentz force changes upon change of reference frames:
| Box 15.1. Writing the force F in terms of forces in the primed reference frame |
|---|
|
To start, we need the transformation for force. We define force by the effect it has on the motion of objects using Newton's second law: F = dp/dt . (15.2) We need the momentum transform from Chapter 11, which to repeat is: where ε is energy as discussed in Chapter 11. Script "E" is used to distinguish energy from electric field. We've also assumed that the velocity V of the reference frame does not change, which also means γ does not change either. We also need the inverse Lorentz transform for time from Chapter 4: Dividing dp by dt gives us the force in Equation (15.2):
Dividing both the numerator and denominator by dt' and replacing the components of dp'/dt' with the corresponding components of F', we have:
We can relate the time derivative of energy in the above equation to force using:
This makes (15.5) become:
Continuing to simply:
|
Next we need to transform the components of u' into corresponding components of u. This may seem like a step backwards, but in the end we need primed variables times unprimed velocities, u, to match the form of (15.1) above where E and B will be functions of E', B' and V (the relative velocity of the primed and unprimed reference frames).
| Box 15.2. Converting the velocities in the primed reference frame to the unprimed frame. |
|---|
|
We start by repeating the transform for velocity from Chapter 9:
The messiest factor in this transform will be converting the u'x in the 1 + u'xV/c2 factor occurring in the denominators of (15.8) to ux. We first transform and simplify this factor:
We use this to transform the u' in (15.8) into corresponding components of u as promised:
We cancel factors as appropriate to write:
|
| Box 15.3. Introducing electric and magnetic fields. |
|---|
|
We next need to substitute the Lorentz force (containing electric and magnetic fields) in for the forces. Just to remind you, the Lorentz force in the primed reference frame is:
When we substitute the various force components of (15.11) into (15.10), F becomes:
This last substitution has reintroduced some primed velocities. We transform these into velocities in the unprimed reference frame using (15.9):
With some rearrangement, this becomes
where a number of terms in the first line have been collected and designated as T given by:
T can be further simplified by the following steps:
Substituting this into (15.14) we have:
|
We need to interpret the above in terms of the standard Lorentz force:
 . (15.17)
. (15.17)
Matching up (15.16) with (15.17), looking at the multipliers of the various velocities, we see that (15.16) will become (15.17) provided that

 . (15.18)
. (15.18)
Summary
Below we have repeated (15.18) as well as a vector notation of the results (in terms of the parallel and perpendicular components). These are the transforms of the electric and magnetic fields to be used when changing from one reference frame to another.
 . (15.19)
. (15.19)
 . (15.20)
. (15.20)




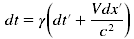
 . (15.4)
. (15.4) . (15.5)
. (15.5) , (15.6)
, (15.6)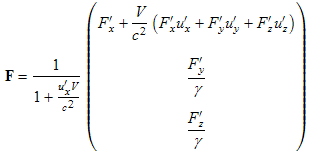 . (15.7)
. (15.7) (15.8)
(15.8) (15.9)
(15.9)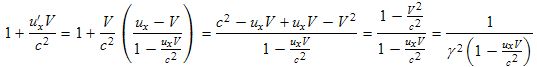
 .
.  (15.10)
(15.10)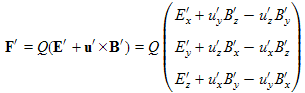 . (15.11)
. (15.11)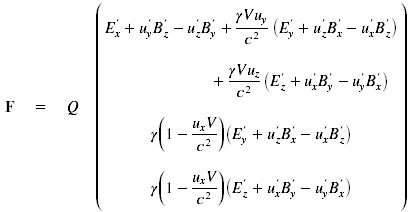 . (15.12)
. (15.12) . (15.13)
. (15.13) (15.14)
(15.14)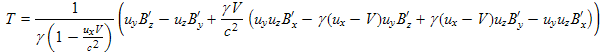 . (15.15)
. (15.15)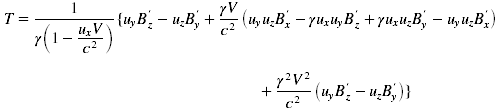



 and
and (15.16)
(15.16)