| all topics by author | introduction to relativity | contents of mathematics of relativity | previous: relativistic mass | next: transforming electromagnetic fields - contents |
11. Relativistic kinetic energy of a particle
If the mass increases with velocity as discussed in the previous chapter, what is the relationship between kinetic energy and velocity?
Classical kinetic energy
In classical (low speed) physics we are taught that the kinetic energy of a particle is given by:
KE = ½mv2 . (11.1)
We can derive this as
where all the vectors are in the forward direction of motion (in the x direction) so we just show these as scalars. Finishing the derivation, we have:
 .
.
(11.3)
Derivation of relativistic kinetic energy
In the relativistic case, we repeat the same steps as above except that now the mass is a function of velocity as given by:
We now repeat the steps in (11.2) and (11.3) with this new non-constant mass that varies with velocity v. This calculation will be more laborious because of this new addition and will take a few lines of equations:
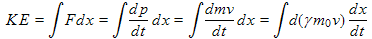 , (11.5)
, (11.5)
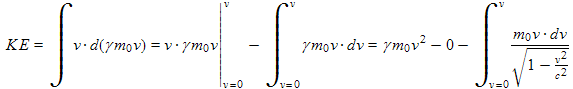 , (11.6)
, (11.6)
where we have used integration by parts for the second step. Also, please excuse the monster integral signs. This is one of the few flaws in the equation editor I use, MathCast, which is otherwise extremely good, especially considering that it is free, very easy to install, and makes entering equations very fast.
 , (11.7)
, (11.7)
where u is defined as:
Continuing with (11.7), we have:
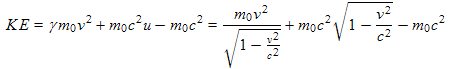 , (11.9)
, (11.9)
and:
Interpretation of relativitic energy
It is standard to call the left-most term of the final expression in (11.10) the "total relativistic energy" or Etotal and the right-most term the "relativistic rest mass energy" or E0:
Making this substitution, we write (11.10) as:
Interpreted this way, the total energy of a particle (or object or mass) has two components, the kinetic energy and the rest mass energy. Identifying E0 as an energy was quite a leap of faith for Einstein, because at the time there was no conceivable way to extract this energy for use or even for experimental verification that this term indeed was an "energy" i.e. an ability to do work. He made the leap primarily because it made a nice equation for the energy as shown in (11.11) above. The ensuing years revealed the annihilation of matter and antimatter, nuclear fission, and nuclear fusion, all of which converted this rest mass energy to the more normal forms of energy (light and heat) verifying his bold assumption.
Incorporating the rest mass into the energy also allowed the energy and the three momentum components (px, py, and pz) to make up a "four vector", a concept we shall briefly explain in Chapter 14.
Momentum/energy transform
We can use our new mass/energy relationship (11.11) to rewrite the momentum/mass transformation, equation (10.25), at the end of the previous chapter as:
where in this equation we represent the total energy of the object (rest energy plus kinetic energy) as E . We have also multiplied the bottom items in (10.25) on either side of the equal sign by c2 .
| all topics by author | introduction to relativity | contents of mathematics of relativity | previous: relativistic mass | next: transforming electromagnetic fields - contents |


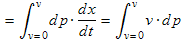
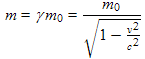
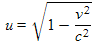

 . (11.10)
. (11.10)



