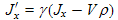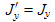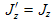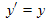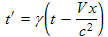|
14. Four-vectors
An astute observer will notice that (13.11) and (13.12) for transforming current and charge densities are operationally the same transforms as we presented earlier for transforming x and t (time). To further emphasize this, we present these two sets of transforms side by side in Table 14.1 below.
Pairings of four quantities that relativistically transform the same as x and t are called four-vectors. The math of four-vectors is well developed and offers a very elegant, compact way to express Maxwell's equations, as well as work with the math of relativity. Their use is often coupled with concepts of matrices, covariant vectors, contravariant vectors, and Einstein's summation convention of repeated indices.
| Table 14.1. Four-vectors | ||
|---|---|---|
| Transform of current and charge | Transform of position and time | Commonly used four-vectors |
|
position and time: (x, y, z, ct) Velocity four-vector: (γvx, γvy, γvz, γc) Momentum and energy:
Current and charge density: (Jx, Jy, Jz, cρ) Vector (magnetic) and scalar (electric) potentials: Four-vector del operator, the d'Alembertian:
| ||
More on four-vectors and how to use them can be found at many web sites and other references. There is a wide variety of conventions used for four-vectors. Some references use the above convention, while others divide the above by a factor of c. Some put the scalar item (last one in each line of the above list) first. Some add the imaginary constant i in front of the scalar item to make the magnitude calculation more "natural". The list in Table 14.1 follows the convention of Lorrain, and Corson. The trick is to be consistent once you start a calculation using four-vectors. One of the most useful four-vector facts is that the "magnitude" of a four-vector (e.g. x2 + y2 + z2 − c2t2) is invariant under change of reference frame. This magnitude is defined as the normal magnitude of the 3-vector part minus the square of the scalar item, i.e. the last item. A very common use of this trick is to apply it to the momentum/energy four-vector: (px, py, pz, E/c). It allows us to equate this magnitude in the frame (the proper frame) where the particle is stationary to another frame in which the particle is moving. In the proper frame the magnitude is -E02/c2 and in the other frame the magnitude equals p2 − E2/c2 . Equating these and multiplying through by c2 yields −E02 = p2c2 − E2 . This equation is useful for relating the momentum p = γm0v of a particle to its total moving energy E = γm0c2 and its rest mass energy E0 = m0c2 . | ||