The pendulum clock

previous: the early clock - verge and foliot

up: home

next: balance wheel clocks

History of Mechanical Clocks with Animations

Fig. 3.1. Galileo Galilei (1564-1642) one of the great scientists, first conceived of the pendulum clock. An Italian, he studied at the University of Pisa, also held a mathematics chair there, and later held a mathematics chair at University of Padua. He is best known for his astronomical observations using the newly invented telescope, his laws of motion, his support of Copernicus's theory of the sun centered solar system, and his trial by the Catholic Church. Wikipedia, fair use policy, tinted.

Figure 3.2. A pendulum consists of a swinging weight, the "bob," held up by a cord or rigid shaft having a pivot. Galileo discovered that the period of a pendulum is mostly determined by its length, the distance from the pivot point to the center of mass of the bob. The pivot point is stationary while the bob swings back and forth as indicated by the bottom arrow.

1.4 The Pendulum Clock

Galileo Galilei (1564 - 1642) is famous for his astronomical observations, his studies of initial motion and free fall, and challenging the Church by his stance in support of Copernicus. However another one of his many pursuits was the pendulum. Legend has it that he was inspired by watching a hanging lantern in his church that would swing as a pendulum during mass. He, like many others, was fascinated by the cyclic motion of this elemental resonator. He determined that the period of a pendulum was independent of the mass of its bob, the swinging weight, and almost independent of the amplitude of its swing. He took this surprising fact to be proof that Aristotle's theory of motion was incorrect and his, Galileo's, theory of uniform motion was instead correct. He further concluded that the pendulum could be the basis for a much improved clock and proceeded to sketch out a design of such a clock as early as 1582 (roughly three centuries after the introduction of the tower clocks in Italy). He wasn't able to find a craftsman willing to build such a clock so it remained only a design. Galileo was very aware that a good clock could solve the longitude problem in navigation. However, instead of pursuing his clock further, his interest turned to his moons-of-Jupiter method as we mentioned earlier. He is reported to have made three unsuccessful trips to King Phillip II of Spain soliciting funds to develop this method.

Animation of Galileo's clock. Mouse over to start.

Galileo's drawing of a pendulum clock. Wikipedia

Figure 3.3. Galileo's pendulum clock design. A weight or spiral spring (not shown) is attached to the lower gear to power the clock. It and the two gears serve to apply a constant clockwise torque to the escapement wheel. The horizontal "S" shaped lever just above the escapement wheel has a hook on its end that fits into the notches in the escapement wheel. This hook is regularly picked up by the upper pallet which is attached to the pendulum to allow the escapement wheel to progress. The lower pallet interacts with the pins on the escapement wheel. The escapement wheel pins pushing on the lower pallet (as shown) nudge the pendulum to keep it going.

The Period of a Pendulum

Galileo discovered that the period of a pendulum depends principally on its length (it also depends on the local acceleration of gravity) and only weakly on anything else that might vary. A potential science fair experiment might involve measuring the period T for different pendulum lengths and comparing with the formula T = 2π√(L/g) where L is the pendulum length and g is the local acceleration of gravity. If you decide to experiment, make sure you have a totally rigid pivot and carefully measure the length to the center of the bob. Keep the swing of the pendulum small (the above formula is only correct for small swings). You might try several lengths and perhaps calculate g from your data. If you routinely travel to locations of differing g's, you might compare you g values with those from a handbook. For more on the pendulum and its use in measuring g see Wikipedia.

---

An actual working pendulum clock

In 1656, 74 years after Galileo's work, Christiaan Huygens, a well know Dutch scientist, turned Galileo's idea into reality and made the first pendulum clock. While Huygens is better known for his work on light waves, challenging and eventually overcoming Isaac Newton's corpuscular theory of light, he is also a very important figure in the history of clocks. In contrast to Galileo's inventing his own escapement mechanism, Huygens used the verge part of the escapement from the earlier tower clocks, replacing only the foliot or resonator with a pendulum. He wisely chose to stay with the perfected design, changing only one feature, resulting in an improved working clock.

Figure 3.4. Christiaan Huygens (1629-1695) of Holland is one of the great scientists of the world. He was a principal figure in the understanding of light, as well as being the inventor of both the pendulum clock and the balance wheel clock. The balance wheel clock saw the most use in the form of pocket watches. Below is his drawing of the pendulum clock.Both images: Wikipedia, Public Domain

Figure 3.5. The escapement and pendulum in Huygens's pendulum clock. This clock uses a verge escapement, but replaces the foliot with a pendulum, greatly improving its accuracy and reliability and reducing its energy needs. The verge is the shaft with two projecting pallets interacting with an escapement wheel (the horizontal wheel with teeth). To accommodate the pendulum's horizontal shaft, he rotated the verge and escapement wheel from their orientation in the verge and foliot design shown earlier.   p. ceperley 2010

The pendulum is a resonator

The pendulum is a simple resonator. While the verge and foliot mechanism also has periodic motion, most experts would not consider it to be a true resonator, certainly not a simple or very good resonator for clock purposes. The ideal resonators for clocks are simple ones containing both a mass and a restoring force that are elemental enough to be perfected to an extreme degree. A pendulum is such a resonator. By adding the pendulum to the prior verge-and-foliot clocks, Huygens added the last missing ingredient for a modern clock: a good resonator.

The chief problem with the verge and foliot mechanism was that it did not have a restoring force. Instead, each cycle involved the toothed wheel pushing weights back and forth in the opposite pivoting directions. This is similar to basing a clock on the time it takes for two tennis players to knock a tennis ball back and forth across the net. How long it would take the tennis ball to complete a cycle would depend on how hard the players were playing, their age, physical strength, where they were on the court, the age of the ball, and tension in the strings in their rackets, etc. Similarly, precisely how long it took the weights in the verge and foliot to go through one cycle depended on how hard the weights were knocked back and forth and this depended on the state of lubrication of the machinery, especially the gear train, the exact state of its wear, how tightly the drive spring was wound up, etc. The process was quite energy consuming as two tennis players might report after a day of hitting the ball back and forth non-stop. It required frequent rewindings, a large drive spring or weights, and furthermore, just like our tennis players might testify, wore out the parts fairly quickly.

The huge improvement that Galileo and Huygens made by adding the pendulum resonator was two-fold. First, to a very large extent, a simple resonator's cycle time is independent of the temperature and state of lubrication, the force which is applied to drive it, and the size of the swing (as long as the swing is reasonably small). Instead, as Galileo observed, a pendulum's period is primarily determined by two very stable parameters: its length and the pull of gravity (technically, g, the local acceleration of gravity). It is affected to a very small degree by those other factors. Thus this resonator provides a much more consistent pacing of the mechanism of a clock.

Secondly, all resonators, including the pendulum, work by recycling energy. While the verge-and-foliot required a strong push each and every half cycle to keep it in motion, a pendulum will swing back and forth many times without any power, and requires only a slight nudge each cycle to sustain it in constant motion. The pull of gravity efficiently turns around the pendulum's motion in one direction and provides motion in the reverse direction. Thus we can understand why a pendulum requires a lot less power which means smaller drive weights and/or less frequent winding. The reduced forces involved result in less wear to the mechanism, making it more reliable. An analogy on the tennis court might be, if after a few days of exhausting constant play, our players attach the tennis ball from a very long cord up to the top of a tree above the tennis court to make a pendulum, and merely nudge the ball every now and then to keeps it swinging back and forth across the net. They would expend a lot less energy, they would wear out much more slowly, and the time required for one cycle of tennis ball motion would become much more consistent.

We might say that the resonator is the most important part of a clock. It is the heart of the clock. It is what parcels out the chunks of time and forces the escapement wheel and the gear train attached to it to turn at a fixed velocity. The other parts of a clock are just there for the "care and feeding" of the resonator. Certainly today, scientists consider the resonator to be the central part of a clock.

The Math of Oscillations Resonators, including the pendulum, and other oscillating devices can be described by trigonometric and complex functions. These form the basis of much of modern electrical engineering and physics. Click here for more details.

Energy in a resonator Energy in a resonator is constantly cycling between two forms. In the case of the pendulum these forms are potential and kinetic energy.

Figure 3.6. Common pendulum clock escapement, the anchor escapement. Mouse over the picture to see it animated. The gray rod goes down to the pendulum weight or "bob" which is not shown here. The rod is attached to the "anchor" (shown in gray) that has two points (or "pallets") which interact with the escapement wheel's sharp teeth. The escapement wheel is driven by a chain of gears attached to a slowly decending drive weight (not shown). The last gear of this chain is shown on the left side of the picture. The escapement wheel would be driven into rapid rotation by this gear train were it not for the points of the anchor that block their rotation and only allow a controlled rotation.

As the pendulum swings to the right, the right point rises and allows the escapement wheel to rotate one half tooth's worth in a clockwise direction, at which time the wheel's motion is blocked by the other point. When the pendulum swings to the left, this other point rises, allowing the escapement wheel to rotate another half tooth's worth clockwise at which time it is blocked by the first point. As each point releases the escapement wheel, the angled tooth surface pushes against the point and gives the anchor and attached pendulum a slight nudge to keep the pendulum swinging.

The escapement

After the resonator, the most complex, and perhaps most intriguing and beautiful, part of a pendulum clock is its escapement mechanism, that part that interfaces between the pendulum and the gear train. As we discussed above, this mechanism must do two things. It must allow the gear train to advance one and only one tooth each swing of the pendulum, and it must also give the pendulum a slight nudge each cycle to sustain its motion. Quite a few different escapements have been developed over the years. Huygens used a verge escapement. A more commonly used escapement for pendulum clocks is the anchor escapement shown in Fig. 3.6. It allows for much smaller pendulum swings which produce more accurate time keeping. (As swings become larger, the period deviates from the constant period of small amplitude swings). This escapement itself comes in many varieties, with the anchor sometimes located above the escapement wheel, sometimes below it, and sometimes to one side of it.

Note that the escapement wheel teeth are rotating with their sloping parts leading, opposite the direction in the verge escapements. As with that earlier escapement, the anchor escapement releases a tooth each half cycle, i.e. at each half swing one end of the anchor releases a tooth and allows the escapement wheel to turn one half tooth's worth. Each time, as the tip of the anchor, the pallet, slides along the sloping side of the wheel, the torque on the escapement wheel from the gear train gives the pendulum a nudge (as a wedge might) in the direction it is moving to sustain its motion. The slope of the escapement wheel's teeth needs to be just right to provide the proper nudge. Also, it is the escapement mechanism that supplies a clock with its tick-tock sound. What we hear is this mechanism releasing the escape wheel, one tooth at a time as the pendulum swings back and forth.

Scroll down a little to see a complete animated pendulum clockworks.

Figure 3.7. Action of the escapement. The pendulum has been shortened in this picture to fit it in. Its pivot point is blue. The red dots show which point of the pallet is engaging the escapement wheel. The escapement wheel turns in the direction of the upper curved arrow powered by weights and a gear train not shown in these pictures. The blue triangle is a stationary visual reference guide to help you see where the bob's equilibrium point is.

In Step 1, the left point of the pallet is engaged. In Step 2, the left point is disengaging, while the right point is engaging. At Step 3, the right point is engaged and the escapement wheel has turned half a tooth clockwise. The sloping teeth of the escapement wheel give the pendulum a slight push during each disengagement.

Note the adjustment screw on the bottom of the bob allows fine adjustment of the pendulum length and thus provides for correction of the clock's speed.

It is very important that the escape mechanism nudges the pendulum the right amount. If the nudging is too weak the pendulum will not be sustain its motion. If too strong, the swings of the pendulum will be too large and the accuracy of the clock will be reduced. If the pendulum has more friction and the nudges are increased to compensate, then the escapement mechanism can force the pendulum to execute its cycle a little faster or slower than it normally would. The ideal situation is for the pendulum to swing with as little friction or damping as possible, be given extremely weak sustaining nudges, and expend extremely little energy on releasing the escape wheel's teeth. If this is the case then the pace of the clock will be set by the pendulum "in isolation" and not by the lubrication or wear of the gears or spring tension or any other effects that are likely to change over time.

While there were efforts to try to reduce the variability in these other effects, it was the improvements in the resonator (the pendulum in this case) that yielded the largest improvements in a clock. As more accurate pendulum clocks were developed, people also found it necessary to "compensate" the pendulum to correct for thermal expansion which will lengthen the pendulum if the temperature should increase. The idea is that a compensated pendulum would have a constant period independent of the temperature it found itself in. Another important aspect is how to adjust the exact cycle time of a clock to correct for the clock being a little slow or fast. It turns out that the pendulum clock is very easy to adjust in speed by merely adjusting the length of its pendulum, usually done with a little, fine-pitched screw in the bob as shown in Figure 3.7.

Figure 3.8. Typical pendulum clockworks. Mouse over this picture to see the animation. The drive weight powers the clock. It applies torque to the gear train, which in turn powers the escapement which regulates the speed at which the gears can turn and the drive weight can descend. The clock hands are also attached to the gears and turn with them. If the clock is properly set up, these hands point to the correct time. This picture shows separate "dials" and sets of numbers for minutes and hours to allow the reader to more clearly see the gears. In practice, the minutes and hours hands are usually mounted on tubular shafts, one inside the other and driven at different rotational rates, so that the minutes and hours hands can share the same dial and same set of numbers.

Decaying Oscillations If a resonator is excited then left alone, the oscillations decay with time. We can learn a lot about the resonator by studying this decay.

Figure 3.9. Pendulum clock by Riefler, circa 1900. The pendulum is in a vacuum to eliminate air friction. This clock represents the peak of accuracy obtained in pendulum clocks. National Institute of Standards and Technology Museum, Public Domain.

Improvements to the pendulum clock

For the next three centuries after Huygens's invention, clockmakers continued to improve the pendulum clock. They learned that the mechanisms of clocks were best made from a combination of brass and iron parts, brass touching iron. The zinc component in the brass provided lubricant and retarded the wear of the gears and escape mechanism. Adding a little lead to the brass improved this further. They also learned to compensate for the slight expansion and contraction of the length of the pendulum due to temperature variations with clever designs which capitalize on differences in expansion rates of various materials. Later clocks where made with invar or even quartz pendulum rods which have very low coefficients of expansion. While the early clocks used large swings of the pendulum, later ones achieved greater accuracy by use of smaller swings. This capitalized on the fact that a pendulum's period is only independent of the swing amplitude for small swings. The escape mechanisms also were repeatedly improved. In 1671 William Clement devised a new anchor or recoil escapement to interfere less with the movement of the pendulum. In 1712 George Graham invented yet a better escape mechanism as well as other improvements which achieved an accuracy of 1 sec/day with his pendulum clock. In 1889, Siegmund Riefler devised a "nearly free pendulum" and achieved an accuracy of 1/100th sec/day, an accuracy of 0.000222% or about 2 parts per million!

The equivalent accuracy in length measurement would be to measure a mile to an accuracy of 1/8 inch (or a kilometer to an accuracy of 2 mm). It seems that the accuracy in making time measurements has always greatly exceeded the accuracy of any other type of measurement. Why is this so? It probably has to do with the built-in, very accurate time keeping that comes with our Earth. Our 6,600,000,000,000,000,000,000 ton (5,980,000,000,000,000,000,000,000 kg or 5.98×1024 kg) planet spins in the vacuum of space at an amazingly constant rate, varying in it's spinning by only about 2 parts per billion per day. This of course is the origin of our "solar time" and we expect, or hope, that our mechanical clocks be of similar accuracy, so that our clocks will agree with solar noon day after day. Before the era of long sea voyages and the need to solve the longitude problem, people were content to merely complain of the inaccuracies in our clocks and reset them every day. At the same time, the resetting reminded them of the inaccuracies of their clocks. There is no built in reminder of the inaccuracies of our length measurement, thus length measurements of one part in a thousand accuracy were considered good up until the last century. The longitude problem required the clocks be made to an accuracy of about a minute per month or 20 parts per million. Once clocks achieved this accuracy then people could effectively use a time measurement to make a longitude determination, i.e. turn a time measurement into a length measurement of sorts. The twentieth century saw even more trickery of this sort, but we are getting ahead of our story.

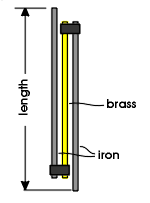
Temperature Compensation Rods of two metals that expand with temperature at different rates were combined to make a pendulum rod whose length does not change with temperature. Click here for more details.

In spite of its great accuracy, the pendulum clock found very limited use aboard ship. This is because the wind and waves caused sailing ships to sway back and forth and this motion interfered with the cycles of the pendulum. A lesser problem was that the period of a pendulum is dependent on the strength of the gravitational constant, which various significantly over the face of the Earth. Huygens, very aware of the great need to determine longitude, put one of his newly invented pendulum clocks aboard a ship, mounting it in a gimbal to reduce swaying. But still, it only performed well in the smoothest of seas. Inventors in pursuit of the marine clock prize looked to replace the pendulum with another similar resonator. That resonator was the balance wheel.

previous: the early clock - verge and foliot

up: home

next: balance wheel clocks