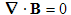| previous - contents of relativity | All postings by author | next - Michelson Morley |
| This posting includes flash animations showing the physics discussed. Most computers have a flash player already installed, but if yours does not, download the free Adobe flash player here. |
A brief history of relativity
Maxwell and the speed of light
In 1861-65 the Scottish physicist, James Clerk Maxwell, derived a set of equations that encapsulated the previous century's research on electric and magnetic effects. These now famous Maxwell equations are still held as the defining equations of electric and magnetic phenomena. In 1864, Maxwell used these equations to show that electric and magnetic interactions can support a wave which travels at the tremendous speed of 300,000 kilometers per second. Since it was known at the time that light traveled at approximately this speed, Maxwell made the correct assumption that his electromagnetic wave was what the common man knew as light.
Maxwell's derivation of his equations was a huge milestone in physics, summing up in an elegant set of equations, lifetimes of toil by experimentalists working with the likes of charged pitch balls, silk threads, lambs wool, frogs' legs, wire, and large messy batteries. None of the experiments involved light. Even today, one and one half centuries later, we cannot do electromagnetic experiments to directly measure the extremely rapidly varying electric and magnetic fields in light, but yet Mr. Maxwell was able to mentally deduce the inner workings of light from the early crude experimental findings.
Speed, relative to what?
The confusing aspect of Maxwell's derivation was that there did not seem to be a reference from which this velocity was to be measured. All other moving things move at a certain speed in reference to something else, often in reference to the Earth. Sound for instance, moves at approximately 0.33 kilometers per second relative to the air through which it is propagating. A moving air mass, i.e. a wind, can add or subtract from the speed that sound travels relative to a stationary person. Figure 3 further illustrates this idea that the velocity of an object is dependent on the velocity of the observer. In this animation, the objects are viewed from three different observers: a shore observer, the surfer, and a sea gull, each moving at different velocities.
Fig. 3. Motions as in the Galilean view of relative frames of reference. Mouse over (or click on if not responding) the animation to start it and mouse off to suspend it. There are three frames of reference in this animation: from the stationary shore, from the surfer, and from the flying seagull's point of view. Click on the three buttons in the lower right corner of the illustration to select each point of view.
The object of all this is to illustrate that the velocity of an object (or wave) is dependent on the reference from which it is being observed. The various objects in the animation move at different velocities in the three different reference frames. |
Waves as disturbances and ether
Except for light and other forms of electromagnetic waves, all classical waves are distortions of some material, distortions that propagate through that material at a certain speed. Since no one could imagine what the material was which light is a distortion of, physicists invented "ether", a mysterious substance that filled all space and through which all objects move. Ether was the fabric of space. Ether was assumed to be unperturbed by the motion of objects, even by objects as massive as the Earth. [This ether is known as ether, aether, æther, or luminiferous aether.]
| Fig. 4. Mechanical waves, such as the waves shown here, are disturbance patterns that maintain their shape and propagate. The media, water in this case, does not move a substantial amount, but instead oscillates in place as the wave passes. The wave is the moving pattern, the moving distortion. Mouse over the figure to see the animation or off to suspend it. If unresponsive, left click on it. The dots and red circles represent objects floating in the water to help you see the motion that the water itself undergoes as the wave passes. For more on water waves see my earlier posting or for more on waves in general see this or this. |
Exactly what is an electric or magnetic field?
The above question (as to what is the media that light is a wave of) is connected with the question of what is an electric field or a magnetic field? After all, it is clear that light is a wave of electric and magnetic fields. Physicists are very familiar with electric and magnetic fields and their effects, but what are these fields at a microscopic level? One odd aspect of Maxwell's equations is that even though they were written for electric and magnetic fields in a vacuum (air is practically the same as a vacuum to these fields), they seem to be perfectly set up to handle electric and magnetic fields in materials where there are microscopic models for exactly how each material affects these fields. In materials, all they require is a slightly different set of coefficients than those for free space, i.e. a vacuum. It is almost as if they are telling us that "free space" is really a material.
It is also odd that light travels through a vacuum. No mechanical wave, such as sound, can traverse an empty vacuum, yet light from the sun has no trouble reaching the Earth through the vacuum of space.
A number of nineteenth century physicists thought that electric and
magnetic fields were some sort of stress or alignment in the underlying
fabric of space, in the ether. With this view, a light wave, being that
it is a wave of electric and magnetic fields, would be a wave (or
pattern) in the stress or alignment of this ether that propagates in a
wave fashion. But what is the velocity of this background ether? After
all, we want to know with respect to what reference frame do we need to
measure the velocity of light.
| previous - contents of relativity | All postings by author | next - Michelson Morley |